Logistic Softmax

Logistic Regression

本章我们来看另一个简单且强大的解决线性回归二元分类问题的算法，即逻辑回归。不要望文生义，逻辑回归虽然带回归这个字眼，但它其实处理的是分类任务，即逻辑回归是一种分类模型，而非回归模型，只不过它本质上使用的是回归, 并且在预测类别的时候采用了回归的思想，所以称为Logistic Regression。

Logistic Regression：

优点：模型简单、输出解释性好且模型输出的结果可解释为概率

缺点：仅适用于二分类问题，对于复杂的非线性问题效果可能不佳。虽然可以用过OvO/OVR的方式拓展到多分类任务，但它其实处理的仍然是二分类问题。

适用场景：适用于二分类或多分类任务，需概率分布的场景，如信用评分、疾病风险评估。

几率(odds)

若将p视为样本x作为正例的可能性，则1-y是其反例的可能性，两者的比值即为几率： \[odds = \frac{p}{1-p}\] 几率反映了x作为正例的相对可能性。

对数几率函数（log odds function）

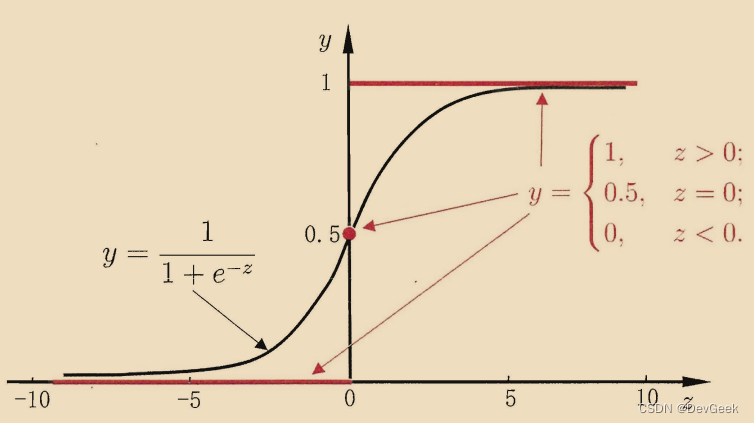
我们的假设函数（这里针对单个样本而言）\(h(x)=\theta^Tx\)的值域是R，同时在这里概率和几率的值域分别为（0， 1）和（0， +inf）。很显然我们不能直接将假设函数产生的值当作概率，所以我们需将概率或几率进行一个函数映射，且这个新的函数的值域为R，定义域为几率的值域。很显然，我们使用几率更容易一些，因为几率的值域刚好与对数函数的定义域相同，所以我们可以对几率取对数，即对数几率（log odds，亦称logit）。且对数几率的值域为R，于是我们就得到了与假设函数相同值域的函数，此时我们就可以将假设函数与对数几率进行对应 \[ln(\frac{p}{1-p})=\theta^Tx=z\] 于是我们就可以求解出概率P \[p=\frac{1}{1+e^{-z}}\] 而这就是对数几率函数也被称为sigmoid函数，该函数将线性模型的输出z映射为（0， 1）之间的概率值，然后参考threshold得到最终的分类结果。

由于 \(e^{-z}\) 是指数函数，其值总是正的，所以 \(e^{-z}\) 加上 1 后也总是大于 1 。因此， sigmoid 函数的分母总是大于 1 ，这意味着整个分数的值永远在 0 和 1 之间，但不会达到这两个端点。换句话说，无论 \(z\) 的值是多少， \(e^{-z}\) 都不可能为负数或零，因此 \(p\) 不可能为 0 或1。

这里我们只是将线性回归的结果输入到sigmoid函数中来计算出样本为正例的概率，所以我们并不将线性回归函数作为目标函数，而是将sigmoid函数作为我们的目标函数。

Logistic Regression的本质

所以LR模型就是通过线性回归对目标的对数几率进行拟合。这就是LR的本质。

sigmoid函数

\[\begin{gathered} p=h_\theta\left(x\right)=g\left(\theta^Tx\right)=\frac1{1+e^{-\theta^Tx}}\quad \quad g(z)=\frac{1}{1+e^{-z}} &\\ g^{\prime}(z)=\left(\frac{1}{1+e^{-z}}\right)^{\prime}=\frac{e^{-z}}{\left(1+e^{-z}\right)^2}=\frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}}=\frac{1}{1+e^{-z}} \cdot\left(1-\frac{1}{1+e^{-z}}\right)=g(z) \cdot(1-g(z))&\end{gathered}\]

\[\begin{aligned} & y=\left\{\begin{array}{l} 1 \\ 0 \end{array}\right. \\ & \widehat{\mathrm{y}}=\left\{\begin{array}{l} 1, p>\text { threshold } \\ 0, p \leq \text { threshold } \end{array}\right. \end{aligned}\] 当某个样本的预测概率\(p\)正好等于我们所设置的阈值\(threshold\)时，我们将该样本预测为正例或者负例都可以。

logistic 回归及似然函数

假设: \[\begin{aligned} & P(y=1 \mid x ; \theta)=h_\theta(x) \\ & P(y=0 \mid x ; \theta)=1-h_\theta(x) \\ & P(y \mid x ; \theta)=\left(h_\theta(x)\right)^y\left(1-h_\theta(x)\right)^{(1-y)} \end{aligned}\]
对于所有训练样本，我们希望最大化整个数据集的联合概率分布，即似然函数: \(L(\theta)=p(\vec{y} \mid X ; \theta)=\prod_{i=1}^m p\left(y^{(i)} \mid x^{(i)} ; \theta\right)\) \[=\prod_{i=1}^m\left(h_\theta\left(x^{(i)}\right)\right)^{y^{(i)}}\left(1-h_\theta\left(x^{(i)}\right)\right)^{\left(1-y^{(i)}\right)}\]
为了便于计算，我们通常对似然函数取对数，得到对数似然函数\(\ell(\theta)\)

\[\ell(\theta)=\ln L(\theta)=\sum_{i=1}^m\left(y^{(i)} \ln h_\theta\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \ln \left(1-h_\theta\left(x^{(i)}\right)\right)\right)\]

交叉熵损失函数

交叉熵损失函数（Cross-Entropy Loss Function），在机器学习中也常称为对数损失（Log Loss），是一种评估模型性能的指标，特别是在分类任务中。它衡量的是实际输出（标签）和模型预测之间的差异。

定义

对于二分类问题，交叉熵损失可以定义为： \[J(\theta)=\sum_{i=1}^m\left[-y^{(i)} \ln \left(h_\theta\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \ln \left(1-h_\theta\left(x^{(i)}\right)\right)\right]\]

其中：

\(m\)是样本数量。
\(y^{(i)}\)是实际的标签，通常是0或1。
\(h_\theta(x^{(i)})\)是模型预测正类的概率。

对于多分类问题，交叉熵损失可以推广为： \[J(\theta)=-\frac{1}{m} \sum_{i=1}^m \sum_{j=1}^k I\left(y^{(i)}=j\right) \ln \left(\frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}}}\right) \quad I\left(y^{(i)}=j\right)= \begin{cases}1, & y^{(i)}=j \\ 0, & y^{(i)} \neq j\end{cases}\] 其中：

k是类别的数量。
\(\frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}}}\)是模型预测第 i个样本属于第 j类的概率。

直观理解

交叉熵起源于信息论，它衡量的是编码事件所需的平均比特数。在机器学习中，它衡量的是模型预测概率分布与真实分布之间的差异。如果模型的预测概率分布接近真实分布，交叉熵损失就会低；反之，如果预测概率分布与真实分布差异很大，交叉熵损失就会高。

为什么使用交叉熵？

概率解释：交叉熵直接与概率相关，使得它成为评估概率输出的自然选择。
梯度优化：与平方误差损失相比，交叉熵在梯度下降中不会那么容易饱和，这意味着即使预测值与实际值差距较大时，梯度也不会变得非常小，这有助于模型的训练。
数值稳定性：通过概率的对数转换，可以避免数值计算问题，如浮点数下溢。

注意事项

交叉熵损失函数要求模型的输出是概率值，这意味着最后一层应该是softmax函数（多分类）或sigmoid函数（二分类）。

最大似然/极大似然函数的随机梯度

\[\begin{gathered} \frac{\partial \ell(\theta)}{\partial \theta_j}=\sum_{i=1}^m\left(\frac{y^{(i)}}{h_\theta\left(x^{(i)}\right)}-\frac{1-y^{(i)}}{1-h_\theta\left(x^{(i)}\right)}\right) \cdot \frac{\partial h_\theta\left(x^{(i)}\right)}{\partial \theta_j} \\ =\sum_{i=1}^m\left(\frac{y^{(i)}}{g\left(\theta^T x^{(i)}\right)}-\frac{1-y^{(i)}}{1-g\left(\theta^T x^{(i)}\right)}\right) \cdot \frac{\partial g\left(\theta^T x^{(i)}\right)}{\partial \theta_j} \\ \quad=\sum_{i=1}^m\left(\frac{y^{(i)}}{g\left(\theta^T x^{(i)}\right)}-\frac{1-y^{(i)}}{1-g\left(\theta^T x^{(i)}\right)}\right) \cdot g\left(\theta^T x^{(i)}\right)\left(1-g\left(\theta^T x^{(i)}\right)\right) \cdot \frac{\partial \theta^T x^{(i)}}{\partial \theta_j} \\ =\sum_{i=1}^m\left(y^{(i)}\left(1-g\left(\theta^T x^{(i)}\right)\right)-\left(1-y^{(i)}\right) g\left(\theta^T x^{(i)}\right)\right) \cdot x_j^{(i)}=\sum_{i=1}^m\left(y^{(i)}-g\left(\theta^T x^{(i)}\right)\right) \cdot x_j^{(i)} \end{gathered}\]

极大似然估计与logistic回归目标函数

我们的目标是最大化对数似然，但在优化问题中，我们通常最小化损失函数。因此，我们取对数似然的负值作为损失函数，即交叉熵损失函数。 \[\begin{aligned} \ell(\theta)=\ln L(\theta) & =\sum_{i=1}^m\left(y^{(i)} \ln h_\theta\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \ln \left(1-h_\theta\left(x^{(i)}\right)\right)\right) \\ 交叉熵损失函数:\\ J(\theta)=-\ell(\theta) & =-\sum_{i=1}^m\left(y^{(i)} \ln h_\theta\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \ln \left(1-h_\theta\left(x^{(i)}\right)\right)\right) \\ & =\sum_{i=1}^m\left[-y^{(i)} \ln \left(h_\theta\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \ln \left(1-h_\theta\left(x^{(i)}\right)\right)\right] \end{aligned}\]

参数θ的求解

Logistic回归 \(\theta\) 参数的求解过程为(类似梯度下降方法):

\[\begin{aligned} & \theta_j=\theta_j+\alpha \sum_{i=1}^m\left(y^{(i)}-h_\theta\left(x^{(i)}\right)\right) x_j^{(i)} \\ & \theta_j=\theta_j+\alpha\left(y^{(i)}-h_\theta\left(x^{(i)}\right)\right) x_j^{(i)} \end{aligned}\]

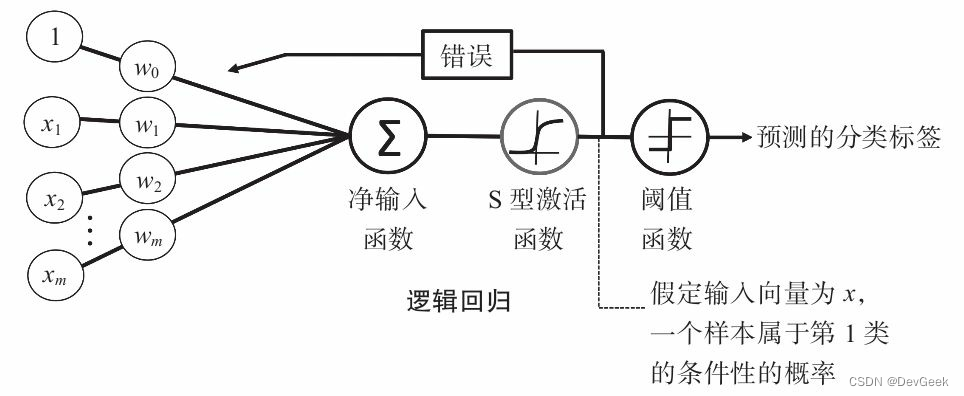
注意Logistic回归是一种分类算法，不能应用于回归中(也即是说对于传入模型的y值（目标变量）来讲，不能是float类型，必须是int类型)

Softmax回归

softmax回归是logistic回归的一般化，适用于K分类的问题，针对于每个类别都有一个参数向量 \(\theta\) ，第 \(k\) 类的参数为向量 \(\theta_k\) ，组成的二维矩阵为 \(\theta_{k^* n}\);

softmax函数的本质就是将一个K维的任意实数向量压缩 (映射) 成另一个K 维的实数向量，其中向量中的每个元素取值都介于 \((0,1)\) 之间。

softmax回归是用于多分类任务的回归算法，其实Softmax回归与逻辑回归相比，只是因为它的参数有多行，每一行参数代表对某一个类别样本概率质量函数的结果。在训练完成后对样本数据集进行预测就可以得到每个样本属于每个类别的概率，样本各个类别概率的总和为1。

因为每一个样本属于一个类别的概率为p，因为有多个类别，这些类别的概率总和为1，所以我们可以用一个函数来将我们的预测结果映射为样本某个类别的概率，于是我们的单个预测值用 \(e^{\theta_K^Tx}\)表示，它不仅极大的放大两个类别的差异，我们之所以使用它，是因为它的值域在（0， +inf），并且它的函数趋势是单调递增的，但因为类别总和要等于1，所以单个类别的预测值要除以整个类别样本的预测值\(\sum_{l}^{k} e^{\theta_l^Tx}\)，如此一来我们就得到了样本每个类别的p，于是我们就得到了softmax回归的概率质量函数。

其实这就相当于最值归一化的过程, 把预测样本每个类别的概率映射到了（0， 1）之间，并且各个类别的样本的概率总和为1。

softmax回归概率函数为：

\[p(y=k \mid x ; \theta)=\frac{e^{\theta_{k}^{T} x}}{\sum_{l=1}^{K} e^{\theta_{l}^{T} x}}, k=1,2 \cdots, K\]

softmax算法原理

softmax函数又称归一化指数函数。它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。下图直观地展现了softmax的计算方法：

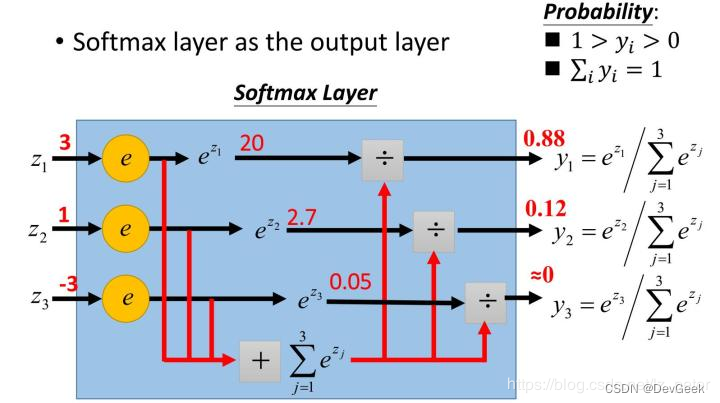
\[p(y=k \mid x ; \theta)=\frac{e^{\theta_{k}^{T} x}}{\sum_{l=1}^{K} e^{\theta_{l}^{T} x}}, k=1,2 \cdots, K\\ h_\theta(x)=\left[\begin{array}{l} p\left(y^{(i)}=1 \mid x^{(i)} ; \theta\right) \\ p\left(y^{(i)}=2 \mid x^{(i)} ; \theta\right) \\ \ldots \\ p\left(y^{(i)}=k \mid x^{(i)} ; \theta\right) \end{array}\right]=\frac{1}{\sum_{j=1}^k e^{\theta_j^T x^{(i)}}}\left[\begin{array}{l} e^{\theta_1^T x} \\ e^{\theta_2^T x} \\ \ldots \\ e^{\theta_k^T x} \end{array}\right] \Rightarrow \theta=\left[\begin{array}{cccc} \theta_{11} & \theta_{12} & \ldots & \theta_{1 n} \\ \theta_{21} & \theta_{22} & \ldots & \theta_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ \theta_{k 1} & \theta_{k 2} & \ldots & \theta_{k n} \end{array}\right]\] 下面为大家解释一下为什么softmax是这种形式。

首先，我们知道概率有三个性质：

非负性: 对于每一个事件A, 有 \(P(A) \geq 0\)
规范性: 对于必然事件S, 有 \(P(S)=1\)
可列可加性: 设 \(A_1, A_2, \ldots\) 是两两互不相容事件, 有 \[P\left(A_1 \cup A_2 \cup \ldots\right)=P\left(A_1\right)+P\left(A_2\right)+\cdots\]

而softmax函数正是利用了概率的非负性和规范性这两个性质，从而将定义域为R的预测结果按照这两种性质转换为概率p。

将预测结果转化为非负数

下图为\(y=e^x\)的图像，我们可以知道指数函数的值域是\((0, +\infin]\)。而softmax第一步就是将回归模型的预测结果映射到指数函数上，如此就保证了概率的非负性。

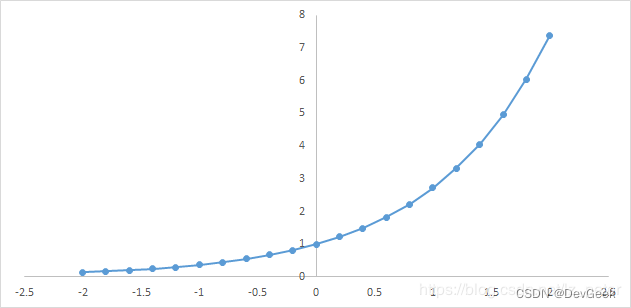
各种预测结果概率之和等于1

为了确保各个预测结果的概率之和等于1，我们只需要将转换后的结果进行归一化处理，具体操作就是将转化后的结果除以转化后所有结果之和，可理解为转化后的结果占总结果的百分比，这样我们就得到了预测样本属于不同的类别的概率。

举一个例子，假如模型对一个三分类问题的预测结果为-3、1.5、2.7。我们要用softmax将模型结果转为概率。步骤如下：

将预测结果转化为非负数

y1 = exp(x1) = exp(-3) = 0.05

y2 = exp(x2) = exp(1.5) = 4.48

y3 = exp(x3) = exp(2.7) = 14.88

各种预测结果概率之和等于1

z1 = y1/(y1+y2+y3) = 0.05/(0.05+4.48+14.88) = 0.0026

z2 = y2/(y1+y2+y3) = 4.48/(0.05+4.48+14.88) = 0.2308

z3 = y3/(y1+y2+y3) = 14.88/(0.05+4.48+14.88) = 0.7666

总结一下softmax如何将多分类输出转换为概率，可以分为两步：

分子：通过指数函数，将实数输出映射到零到正无穷。
分母：将所有结果相加，进行归一化。

下图为斯坦福大学CS224n课程中对softmax的解释：

Q：我们为什么把目标函数转化为指数的形式，而不是平方的形式呢？🧐

这是因为\(e^{\theta_k^Tx}\)，它在定义域R上是单调递增的函数，而\(\frac{(\theta_k^Tx)^2}{\sum_{l=1}^{k}(\theta_k^Tx)^2}\), 它是一个关于y轴对称的函数，这意味着如果两个互为相反数的\(\theta_k^Tx\)，它们的概率是相同的，而我们的思想是回归模型得出的那个值越大，那么它属于某一类别的概率越大，而平方形式的目标函数显然与我们的思想相冲突。

在使用指数函数作为线性回归的映射函数主要是原因它的性质能够帮助我们在多类别分类问题中得到规范化的概率分布。

指数函数具有以下一些重要性质：

非负性：对于任何实数 x，指数函数 \(e^x\) 的值都是非负的。这对于表示概率非常重要，因为概率值必须始终为非负值。
增长性：指数函数的值随着输入的增加而增加。这对于模型输出的解释和比较是有帮助的，因为高于其他类别的概率值将更大。
敏感性：指数函数对于输入变化的变化非常敏感。这有助于模型在不同类别之间建立明显的区分度，以便我们可以更好地区分不同的类别。

通过应用指数函数，我们可以将原始的预测值转换为正值，然后使用归一化（除以总和）来获得概率分布。这样，Softmax函数能够将实数向量转换为表示多个类别的概率分布。

softmax函数损失函数

\[J(\theta)=-\frac{1}{m} \sum_{i=1}^m \sum_{j=1}^k I\left(y^{(i)}=j\right) \ln \left(\frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}}}\right) \quad I\left(y^{(i)}=j\right)= \begin{cases}1, & y^{(i)}=j \\ 0, & y^{(i)} \neq j\end{cases}\]

在给出的更新公式\(I(y^{(i)}=j)\)表示一个指示函数（Indicator Function）。它在逻辑斯蒂回归中用于判断样本的真实标签是否等于\(j\)。

指示函数（Indicator Function）是一种函数，当某个条件成立时返回1，否则返回0。在这里，\(I(y^{(i)}=j)\)的作用是判断样本\(i\)的真实标签\(y^{(i)}\)是否等于\(j\)，如果等于\(j\)，则返回1，表示样本\(i\)属于类别\(j\)，否则返回0。

换句话说，\(I(y^{(i)}=j)\)是一个二进制函数，用于标识样本是否属于特定类别。在给定的更新公式中，它用于计算属于类别\(j\)的样本的特征向量加权和。

softmax算法梯度下降法求解

\[\begin{align*} & \frac{\partial}{\partial \theta_j} J(\theta) = \frac{\partial}{\partial \theta_j} -I\left(y^{(i)}=j\right) \ln \left(\frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}}}\right) \\ & = \frac{\partial}{\partial \theta_j} -I\left(y^{(i)}=j\right)\left(\theta_j^T x^{(i)}-\ln \left(\sum_{l=1}^k e^{\theta_l^T x^{(i)}}\right)\right) \\ & = -I\left(y^{(i)}=j\right)\left(1-\frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}}}\right) x^{(i)}\\ &\theta_j=\theta_j+\alpha\sum_{i=1}^mI\Big(y^{(i)}=j\Big)\Big(1-p\Big(y^{(i)}=j\Big|x^{(i)};\theta\Big)\Big)x^{(i)}\\ &\theta_j=\theta_j+\alpha I\Big(y^{(i)}=j\Big)\Big(1-p\Big(y^{(i)}=j\Big|x^{(i)};\theta\Big)\Big)x^{(i)} \end{align*}\]

总结

线性模型一般用于回归问题，Logistic和Softmax模型一般用于分类问题。
求θ的主要方式是梯度下降算法，梯度下降算法是参数优化的重要手段，主要是SGD，适用于在线学习以及跳出局部极小值。
Logistic/Softmax回归是实践中解决分类问题的最重要的方法。
广义线性模型对样本要求不必须服从正态分布，只需要服从指数分布簇（二项分布、泊松分布、伯努利分布、指数分布等）即可；广义线性模型的自变量可以是连续的也可以是离散的。

动手实现一个逻辑回归代码

以上就是我们本章所要讲解的内容，为了能够使我们更好地理解逻辑回归的工作原理，我们接下来就动手实现一个简单的逻辑回归算法。由于该算法的性能度量指标是准确度(accuracy)，而该指标计算思路很简单，所以我们不妨也将该指标进行一个实现。 accuracy_score方法封装在本地的Ml_master包下的metrics.py模块中

import numpy as np


def accuracy_score(y_true, y_predict):
    """
    计算y_true和y_predict之间的准确度

    :param y_true: 测试数据集中的数据
    :param y_predict: 模型预测的结果
    :return: 算法的分类准确度
    """
    y_true, y_predict = np.asarray(y_true), np.asarray(y_predict)
    assert y_true.shape[0] == y_predict.shape[0], \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(y_predict == y_true) / len(y_true)

接下来开始实现LogisticRegression算法： LogisticRegression类封装在本地的Ml_master包下的LogisticRegression.py模块中

import numpy as np
from .metrics import accuracy_score
from sklearn.preprocessing import OneHotEncoder


class LogisticRegression:
    """Logistic Regression Classifier using batch gradient descent.

    Parameters:
    -----------
    :param: C:惩罚项系数， C的倒数即正则化强度
    :param: n_iters: 最大梯度迭代次数
    :param: penalty: 惩罚项， 可选'l1'或'l2'
    """

    def __init__(self, penalty='l2', C=1.0, n_iters=1e4):
        self.C = C
        self.n_iters = n_iters
        self.multi_class = None
        self._theta = None
        self.coef_ = None
        self.intercept_ = None
        self.penalty = penalty

    @staticmethod
    def _sigmoid(z):
        return 1. / (1 + np.exp(-z))

    @staticmethod
    def _softmax(z):
        # 为了数值稳定性，减去每行的最大值
        exp_shifted = np.exp(z - np.max(z, axis=1, keepdims=True))
        probabilities = exp_shifted / np.sum(exp_shifted, axis=1, keepdims=True)
        return probabilities

    def __compute_pena_v(self, theta):
        """计算正则化项的值
        """
        if self.penalty == 'l2':
            pena_val = (1 / self.C) * np.sum(theta ** 2)
        elif self.penalty == 'l1':
            pena_val = (1 / self.C) * np.sum(np.abs(theta))
        else:
            raise ValueError('penalty must be l1 or l2')
        return pena_val

    def __compute_pena_d(self, theta):
        """计算正则化项的导数
        """
        if self.penalty == 'l2':
            pena_d = 2 * (1 / self.C) * np.sum(theta)
        elif self.penalty == 'l1':
            pena_d = (1 / self.C) * np.sum(np.sign(theta))
        else:
            raise ValueError('penalty must be l1 or l2')
        return pena_d

    def fit(self, X_train, y_train):
        assert X_train.shape[0] == y_train.shape[0], \
            'the size of X_train must be equal to the size of y_train'
        # 以确保数据处理的一致性，我们将输入的数据统一转化为NumPy数组进行数值计算
        X_train, y_train = np.asarray(X_train, dtype=np.float64), np.asarray(y_train, dtype=np.int32)
        # 通过目标变量的类别数判断我们所要处理的问题是否是多分类问题
        self.multi_class = True if len(np.unique(y_train)) > 2 else False
        if self.multi_class:
            self._fit_multi(X_train, y_train)
        else:
            self._fit_bin(X_train, y_train)

    def _fit_bin(self, X_train, y_train):
        """二分类问题的拟合函数"""
        # 计算损失函数
        def j(theta, X_t, y):
            # 计算每一个样本在当前theta下预测为正例的概率
            y_probs = self._sigmoid(X_t @ theta)
            try:
                return - np.sum(y * np.log(y_probs) + (1 - y) * np.log(1 - y_probs)) + self.__compute_pena_v(theta)
            except RuntimeWarning:
                return float('inf')

        # 求偏导计算平均梯度
        def dj(theta, X_t, y):
            return (X_t.T @ (y - self._sigmoid(X_t @ theta)) + self.__compute_pena_d(theta)) / len(y)

        def gradient_descent(X_t, initial_theta, epsilon=1e-8):

            # 动态学习率
            def learning_rate(t):
                """t指的是迭代次数"""
                return 5 / (t + 50)

            theta = initial_theta
            cur_iter = 0
            while cur_iter < self.n_iters:
                gradient = dj(theta, X_t, y_train)
                last_theta = theta
                # 这里不能使用theta += learning_rate(cur_iter) * gradient， 因为+=运算是原地对数组进行操作， 而last_theta引用指向theta的地址，
                # 这会导致theta == last_theta
                theta = theta + learning_rate(cur_iter) * gradient
                if abs(j(last_theta, X_t, y_train) - j(theta, X_t, y_train)) < epsilon:
                    break
                cur_iter += 1
            return theta

        # 对原始训练数据集添加偏置项
        X_b = np.hstack([np.ones([X_train.shape[0], 1]), X_train])
        # 初始化theta
        init_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, init_theta)
        self.coef_ = self._theta[1:]
        self.intercept_ = self._theta[0]

        return self

    def _fit_multi(self, X_train, y_train):
        """多分类问题的拟合函数"""
        one_enc = OneHotEncoder(handle_unknown='ignore', dtype=int)
        # 为了方便后续计算训练样本预测为实际类别所对应的概率， 我们对目标变量进行one-hot编码化
        y_onehot = one_enc.fit_transform(y_train.reshape(-1, 1)).toarray()
        # 获取one-hot编码后的目标变量每一列所对应的类别
        target_cats_ = one_enc.categories_[0]
        n_target_cats = len(target_cats_)

        # 计算损失函数
        def j(theta, X_t):
            y_probs = self._softmax(X_t @ theta.T)
            try:
                return - np.sum(y_onehot @ np.log(y_probs).T) + self.__compute_pena_v(theta)
            except RuntimeWarning:
                return float('inf')

        # 求偏导计算平均梯度
        def dj(theta, X_t, y):
            # 计算训练样本属于不同类别的概率
            y_pred = self._softmax(X_t @ theta.T)
            return ((y_onehot * (1 - y_pred)).T @ X_t + self.__compute_pena_d(theta)) / len(y)

        def gradient_descent(X_t, initial_theta, epsilon=1e-8):

            def learning_rate(t):
                """t指的是迭代次数"""
                return 5 / (t + 50)

            theta = initial_theta
            cur_iter = 0
            while cur_iter < self.n_iters:
                gradient = dj(theta, X_t, y_train)
                last_theta = theta
                # 这里不能使用theta += learning_rate(cur_iter) * gradient， 因为+=运算是原地对数组进行操作， 而last_theta引用指向theta的地址，
                # 这会导致theta == last_theta
                theta = theta + learning_rate(cur_iter) * gradient
                if abs(j(last_theta, X_t) - j(theta, X_t)) < epsilon:
                    break
                cur_iter += 1
            return theta

        X_b = np.hstack([np.ones([X_train.shape[0], 1]), X_train])
        init_theta = np.ones((n_target_cats, X_b.shape[1]))
        self._theta = gradient_descent(X_b, init_theta)
        self.coef_ = self._theta[:, 1:]
        self.intercept_ = self._theta[:, 0]

        return self

    def predict_proba(self, X_test):
        assert self._theta is not None, \
            'must fit before predict'
        if self.multi_class:
            assert X_test.shape[1] == self.coef_.shape[1], \
                'the feature number X_test must be equal to X_train'

            X_b = np.hstack([np.ones([X_test.shape[0], 1]), X_test])
            return self._softmax(X_b @ self._theta.T)
        else:
            assert X_test.shape[1] == len(self.coef_), \
                'the feature number X_test must be equal to X_train'

            X_b = np.hstack([np.ones([X_test.shape[0], 1]), X_test])
            return self._sigmoid(X_b @ self._theta)

    def predict(self, X_test, threshold=0.5):
        assert self._theta is not None, \
            'must fit before predict'
        if self.multi_class:
            assert X_test.shape[1] == self.coef_.shape[1], \
                'the feature number X_test must be equal to X_train'
            proba = self.predict_proba(X_test)
            return np.argmax(proba, axis=1)
        else:
            assert X_test.shape[1] == len(self.coef_), \
                'the feature number X_test must be equal to X_train'

            proba = self.predict_proba(X_test)
            return np.array(proba >= threshold, dtype=int)

    def score(self, X_test, y_test):
        y_pred = self.predict(X_test)
        return accuracy_score(y_test, y_pred)

    def __repr__(self):
        return "LogisticRegression()"

至此我们就完成对逻辑回归算法的简单复现工作，接下来我们对该算法进行测试。我们在这里使用sklearn中的数字数据集。
首先, 导入我们所需要的模块：

import numpy as np
from sklearn.datasets import load_digits
from ML_master.model_selection import train_test_split
from ML_master.LogisticRegression import LogisticRegression

载入数据

# 加载数据
data = load_digits()
X = data.data
y = data.target
print(X.shape, y.shape)  # (1797, 64) (1797,)

将原始数据按比例分为训练集和测试集（这里我们使用的是上一篇文章封装好的train_test_split方法, 而非sklearn封装的train_test_split方法。对该方法的实现感兴趣的同志可以戳这里直达上篇文章）

1	`X_train, X_test, y_train, y_test = train_test_split(X, y, test_ratio=0.2, seed=666)`

创建一个逻辑回归分类器，并拟合训练数据

1 2	`log_reg = LogisticRegression(C=100000, penalty='l1') log_reg.fit(X_train, y_train)`

对该模型的性能进行评估

1
2
3

train_score = log_reg.score(X_train, y_train)
test_score = log_reg.score(X_test, y_test)
print(f'训练集准确度: train_score:{train_score}\t测试集准确度: test_score:{test_score}')

评估结果:

1	`训练集准确度: train_score:0.9499304589707928 测试集准确度: test_score:0.9303621169916435`

相信大家到这里就已经理解了逻辑回归的大致工作原理，那么接下来我们就可以使用sklearn中已经为我们封装好的逻辑回归算法来对鸢尾花的类别进行预测。

首先导入我们所需要的模块：

 import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from matplotlib.colors import ListedColormap

1 2	`mpl.rcParams['font.sans-serif'] = ['simHei'] mpl.rcParams['axes.unicode_minus'] = False`

载入数据：

# 加载数据
data = load_iris()

# 为了方便可视化，我们只取[1, 3]两个特征
X = data.data[:, [1, 3]]
y = data.target

将原始数据按比例分为训练集和测试集（这里我们使用的是sklearn中的train_test_split方法)。

1	`X_train, X_test, y_train, y_test = train_test_split(X, y, test_ratio=0.2, seed=666)`

创建一个逻辑回归实例对象，接着拟合我们的训练数据

log_reg = LogisticRegression(max_iter=int(1e4), penalty='l2', n_jobs=-1, C=100000)
"""
    penalty='l2', 过拟合解决参数,l1正则或者l2正则 {'l1', 'l2', 'elasticnet', 'none'}, default='l2'；'newton-cg'、'sag' 和 'lbfgs' 求解器仅支持 l2 惩罚。'elasticnet' 仅由 'saga' 求解器支持。如果为“无”（不受 liblinear 求解器支持），则不应用正则化。
    dual=False, 
    tol=1e-4, 梯度下降停止条件
    C=1.0, 正则化强度的倒数；必须是正浮点数。较小的值指定更大的正则化
    fit_intercept=True, 
    intercept_scaling=1, 
    class_weight=None, 类别权重，有助于解决数据类别不均衡的问题
    random_state=None, 
    solver='liblinear',  参数优化方式，当penalty为l1的时候，参数只能是：liblinear(坐标轴下降法)；当penalty为l2的时候，参数可以是：lbfgs(拟牛顿法)、newton-cg(牛顿法变种)，sag(minibatch),维度<10000时，lbfgs法比较好， 维度>10000时， cg法比较好，显卡计算的时候，lbfgs和cg都比seg快【nlbfgs和cg都是关于目标函数的二阶泰勒展开】
    max_iter=100, 最多的迭代次数
    multi_class='ovr', 分类方式参数；参数可选: ovr(默认)、multinomial；这两种方式在二元分类问题中，效果是一样的；在多元分类问题中，效果不一样；ovr: one-vs-rest， 对于多元分类的问题，先将其看做二元分类，分类完成后，再迭代对其中一类继续进行二元分类；multinomial: many-vs-many（MVM）,即Softmax分类效果
    verbose=0, 
    warm_start=False, 
    n_jobs=1 
"""

# 训练模型
log_reg.fit(X_train, y_train)

评估模型:

1 2	`print('train_set_score:', log_reg.score(X_train, y_train)) # 所有的分类器的score默认评估指标是准确率 print('test_set_score:', log_reg.score(X_test, y_test))`

评估结果:

1 2	`train_set_score: 0.9416666666666667 test_set_score: 1.0`

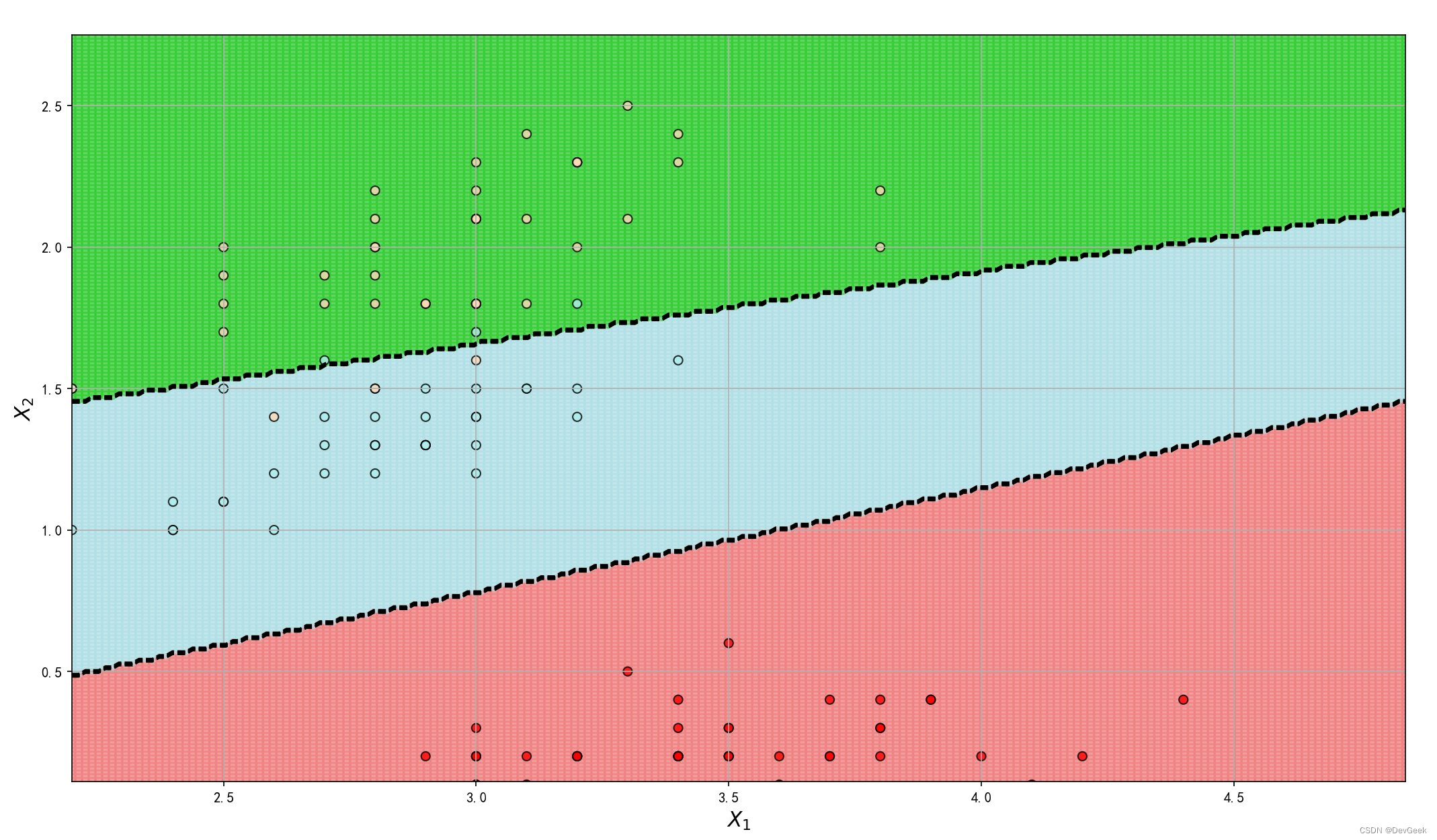
接着我们绘制一下各个类别的决策边界，我们首先定义一个可视化决策边界的方法：

def decision_boundary(X_d, y_d, clf):
    ### 绘制决策边界
    ax1_min, ax2_min = np.min(X_d, axis=0) + np.min(X_d, axis=0) * 0.1
    ax1_max, ax2_max = np.max(X_d, axis=0) + np.max(X_d, axis=0) * 0.1
    xx1, xx2 = np.meshgrid(np.linspace(ax1_min, ax1_max, int(ax1_max - ax1_min) * 100),
                           np.linspace(ax2_min, ax2_max, int(ax2_max - ax2_min) * 100))
    X_new = np.stack((xx1.ravel(), xx2.ravel()), axis=1)
    y_pred = clf.predict(X_new)
    zz = y_pred.reshape(xx1.shape)
	
    custom_cmap = ListedColormap(['#F08080', '#B0E0E6', '#32CD32'])
    custom_dark = ListedColormap(['r', '#AFEEEE', '#FFDAB9'])
    plt.scatter(xx1, xx2, c=zz, cmap=custom_cmap, alpha=0.5)
    # 绘制决策边界
    plt.contour(xx1, xx2, zz, colors='k', linestyles='--')
    plt.scatter(X_d[:, 0], X_d[:, 1], s=40, c=y_d, cmap=custom_dark, edgecolors='k', alpha=0.8)
    plt.xlabel('$X_1$', fontsize=15)
    plt.ylabel('$X_2$', fontsize=15)
    plt.xlim((ax1_min, ax1_max))
    plt.ylim((ax2_min, ax2_max))
    plt.grid(True)
    plt.subplots_adjust(hspace=0.5)
    plt.show()

调用决策边界绘制函数

1	`decision_boundary(X_train, y_train, log_reg)`

在这里插入图片描述下面是关于sklearn中LogisticRegression算法的solver参数的一个拓展内容： 拓展-快速了解机器学习中LogisticRegression里的五种solver优化参数（超详细)

参考文献

【1】西瓜书，周志华【2】http://t.csdnimg.cn/bWCHe

Algorithm > Machine Learning > Artificial Intelligence > Data Science

#Machine Learning #Algorithm #Logistic Regression #Softmax Regression

Logistic Softmax

https://devgek.cn/2024/04/07/Logistic-Softmax/

Author

DXGEK

Posted on

April 7, 2024

Licensed under

Recommended system common algorithm Previous

Gradient Descent Next

Logistic Softmax

Logistic Regression

几率(odds)

对数几率函数（log odds function）

sigmoid函数

logistic 回归及似然函数

交叉熵损失函数

最大似然/极大似然函数的随机梯度

极大似然估计与logistic回归目标函数

参数θ的求解

Softmax回归

softmax算法原理

Q：我们为什么把目标函数转化为指数的形式， 而不是平方的形式呢？🧐

softmax函数损失函数

softmax算法梯度下降法求解

总结

动手实现一个逻辑回归代码

参考文献

Q：我们为什么把目标函数转化为指数的形式，而不是平方的形式呢？🧐