Recommendation system project arrangement and knowledge review

整体规划

重点: 业务/场景 + 工程 + 算法

1. 以项目为导向，最终掌握企业中实际常用算法，包括但不限于：协同过滤、MF、FM、 FFM、LR、GBDT、（Youtube Net、DSSM、Wide&Deep、DeepFM；使用的都是FC全连接）、xDeepFM、DIN、DIEN、 DSIN、FiBiNet、bert4rec、ESMM、MMOE、PLE等;

• 介绍推荐系统的整体结构以及各个组件的常用实现方式;
• 介绍推荐系统的常用部署方式以及具体部署方式;

经典数据结构算法

• 数据结构：数组、链表、堆栈、队列、树；
• 常用算法：回溯法、分治法、动态规划、贪心算法、分支限界法、二分查找法；
• 排序算法：冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、桶排序、基数排序；
• 参考： https://leetcode.cn/ https://www.cnblogs.com/mq0036/p/7940728.html http://www.cnblogs.com/libra-yong/p/6390303.html https://blog.csdn.net/Selenitic_G/article/details/87978673

知识回顾

• 通用基础知识：欠拟合、过拟合、通用评估方式、常用特征工程(OneHot、分桶/分箱/分区、Hashing、Log、特征缩放、标准化等)等；

为什么有时我们要对连续型数据做分箱操作呢？

在一些模型中，对离散型数据的处理比对连续型数据更为高效， 连续型特征相对于离散型特征较难学习。通过分箱操作，可以将连续型数据转换为离散型数据，降低了模型学习的计算复杂度，使得模型更容易进行学习和推断。并且在一些业务场景下， 比较适合使用分箱。

除此之外， 对连续型数据进行分箱操作还有几个主要原因：

1. 简化模型： 连续型数据可能包含丰富的信息，但有时候我们可能更感兴趣的是数据的整体趋势而不是精确的数值。分箱操作可以将连续数据转换为有序的离散类别，从而简化模型的复杂度。
2. 处理异常值： 分箱操作可以减少某些异常值的影响。将数据进行分箱后，在每个箱子里的数据点更可能受到相似的影响，这样就可以减少某些极端值对模型的影响。
3. 特征交互： 在一些模型中（比如逻辑回归），分箱可以帮助捕捉特征之间的非线性关系。通过分箱可以引入交互项，增加了模型的表达能力。
4. 满足模型的假设： 有些模型对输入的数据具有一定的假设，比如线性回归中的自变量需要满足线性关系。通过分箱操作，可以更好地满足这些假设。
5. 可解释性： 在有些情况下，离散的特征更容易解释和理解。分箱操作可以帮助将连续型数据转换为人们更容易理解和分析的形式。

例如;对年龄特征进行分箱，在判断人们是否经常使用电脑办公这样的场景中就非常有用。首先，分箱操作提高了模型的解释性，使我们更容易理解不同年龄段与电脑使用偏好之间的关系。其次，这种操作有助于捕捉年龄与电脑偏好之间的非线性关系，从而提高了模型的预测能力。此外，分箱也有助于处理异常值，增强模型的鲁棒性。最重要的是，通过分箱后的结果，我们能够更好地利用可视化图表展示不同年龄段对电脑使用的影响，帮助业务人员更好地理解模型的影响因素。因此，对年龄特征进行分箱操作有利于提高模型的效果，并更好地满足业务需求。

我们看一下不分箱的这种情况， 假设现在age特征所对应的参数为w， 那么与之所对应的线性回归方程就是这个样子\(z=...+w\cdot age + ...\)， 结合现实的场景， 我们不免会认为， 在10岁以下和60岁往上的人群中，普遍是不使用电脑进行办公的， 用图来表示大化大概就是这样：

image-20240503173004374

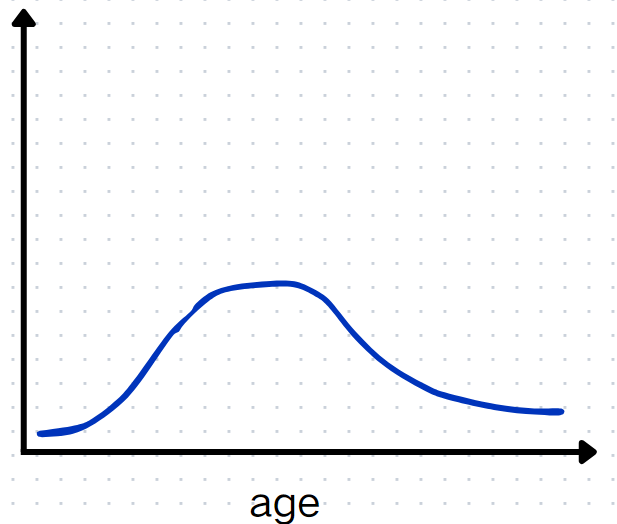
当年龄越小于10岁或者越大于60我们希望z的值越小， 于是此时w的值偏小。而当年龄处于20-40岁这个范围时很可能年龄越大， 使用电脑的频率越高， 于是我们就希望在此范围内， 年龄越大w越大。假设我们根据一个60岁的人计算出了一个w值， 但是这个参数的值并不能被我们拿来去预测20-40岁左右的人群， 当我们训练的过程中损失函数就很有可能出现抖动的情况， 无法学习到一个合适的参数， 也就是说这种情况下， 不同age的人争夺同一个w值， 即age特征中的值会互相排斥。所以我们要做一个分箱， 分箱之后再做一个One-hot， 这样我们就可以针对不同类别的人群来学习相对应的参数w， 且不同年龄段的人群间没有干扰了。

• 机器学习算法：LR、GBDT、XGBoost、KD-Tree(最基础的近邻算法)等；
• 深度学习算法：MLP（普通的全连接神经网络）、LSTM、Attention等；

LR

LR：逻辑回归算法，是机器学习领域中常用的线性分类算法； \[\begin{aligned} & \hat{y}=\operatorname{sigmoid}(w x+b) \\ &p=h_\theta\left(x\right)=g\left(w x+b\right)=\frac1{1+e^{-(w x+b)}}\\ & \text { loss }=\sum_{i=1}^m\left[-y^{(i)} \ln \left(h_\theta\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \ln \left(1-h_\theta\left(x^{(i)}\right)\right)\right] \\ & \dot{w}=w-\alpha * \frac{\partial \text { loss }}{\partial w} \\ & \dot{b}=b-\alpha * \frac{\partial l o s s}{\partial d} \end{aligned}\]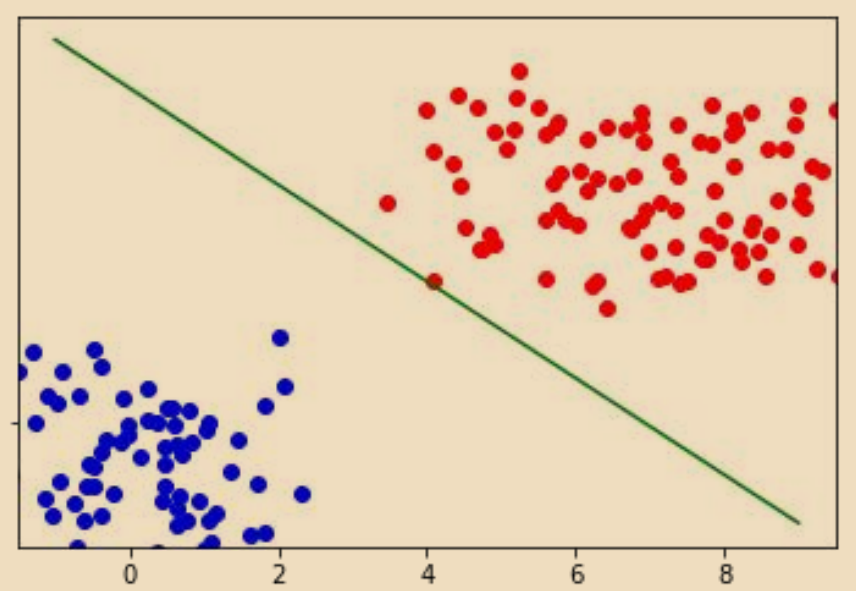

GBDT、XGBoost

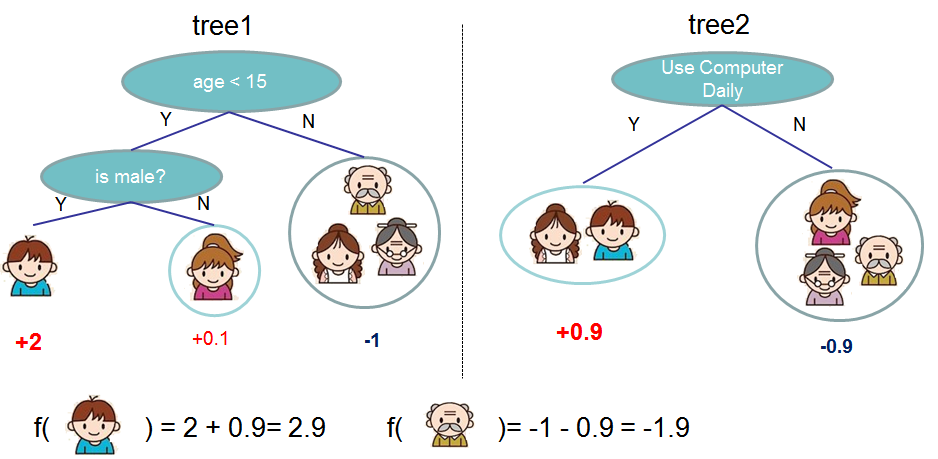
• GBDT: 一种基于决策树的Boosting算法，利用残差的思路让损失函数在不同的子模型构建过程中越来越小的过程就是GBDT的构建过程；
• XGBoost: 是一个GBDT的优化，构建速度更快，更加不容易过拟合；

image-20240503155619099

KDTree

KDTree: 一种最基本的近邻样本搜索算法，利用方差的特性将数据从最大方差的维度进行分割， 从而保证数据能够尽可能的分割开，从而提高检索速度(减少比较次数)。

image-20240503155713010

image-20240503155717348

image-20240503155721243

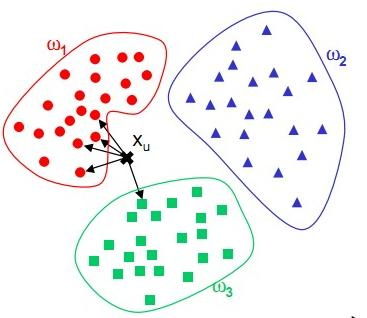
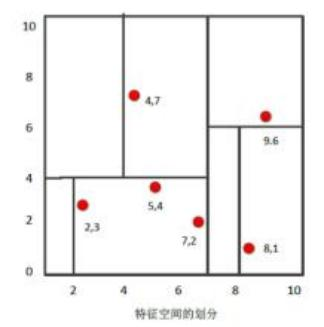
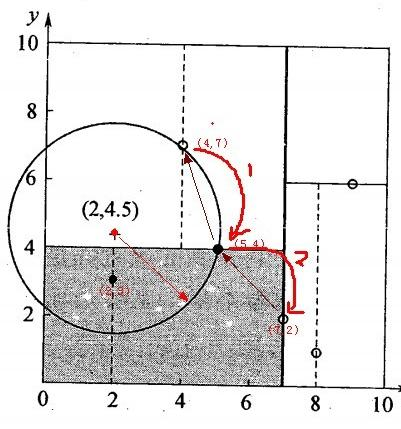
KD_Tree的最近邻域搜索的策略其实与K-means在检索最近邻的样本中有些相似之处：

• 空间划分：KD树通过递归地在K维空间中划分数据，创建了一种数据结构，使得可以快速检索到与查询点最近的点。K-means通过将数据划分为K个簇来组织数据，每个簇的中心代表了该簇中所有点的中心位置。在检索时，可以先找到最近的簇中心，然后在该簇中搜索最近的点。
• 减少计算量：两种方法都旨在通过某种形式的空间划分或组织来减少在大数据集中找到最近邻或相似项的计算量。

如果我们将K-means用于最近邻搜索，它可能会引入更大的误差，因为它基于簇中心来估计相似性，而不是基于实际的最近邻距离。而KD树提供了一种精确的最近邻搜索方法，不会因为算法本身的原因而引入误差。

MLP

MLP：多层感知机/全连接神经网络，可以认为是最基础的神经网络机构，可以认为只有全连接结构。

我们可以将多层感知机和全连接神经网络视为同一个东西。

image-20240503155754360

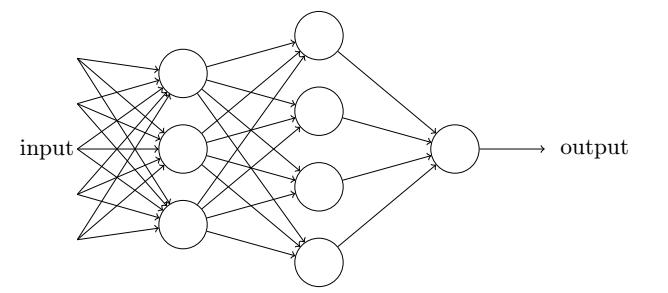
神经元的核心功能之一是特征提取，这一过程中，主要涉及调整神经元内部的权重。而神经元通过激活函数，对输入的加权和进行非线性转换，从而实现特征的提取和非线性映射。

在训练过程中，通过反向传播算法调整模型的参数（即权重和偏置），通过参数逐步学习进而获得能够表示特定特征的能力，即使得神经元能够捕捉到数据中的关键特征，同时最小化样本的损失。随着训练的进行，这些调整后的参数将能够逐渐组合起来，从而使得模型能够对样本进行更准确的预测或分类， 即针对特定样本最小化损失。

因此，当模型在特定业务场景中通过参数学习到了特定的特征信息时，我们就认为神经元已经可以很好的提取出数据中蕴含的特征信息。在这个过程中，神经元通过参数的学习和调整，进而有效地掌握了数据中的关键特征，从而使得模型能够对样本进行更加准确的预测。

LSTM

LSTM是RNN体系中一个非常重要而成熟的结构，通过门的结构来对信息进行有针对性的保留， 从而缓解了RNN结构中的长序列依赖问题；

image-20240503155845884

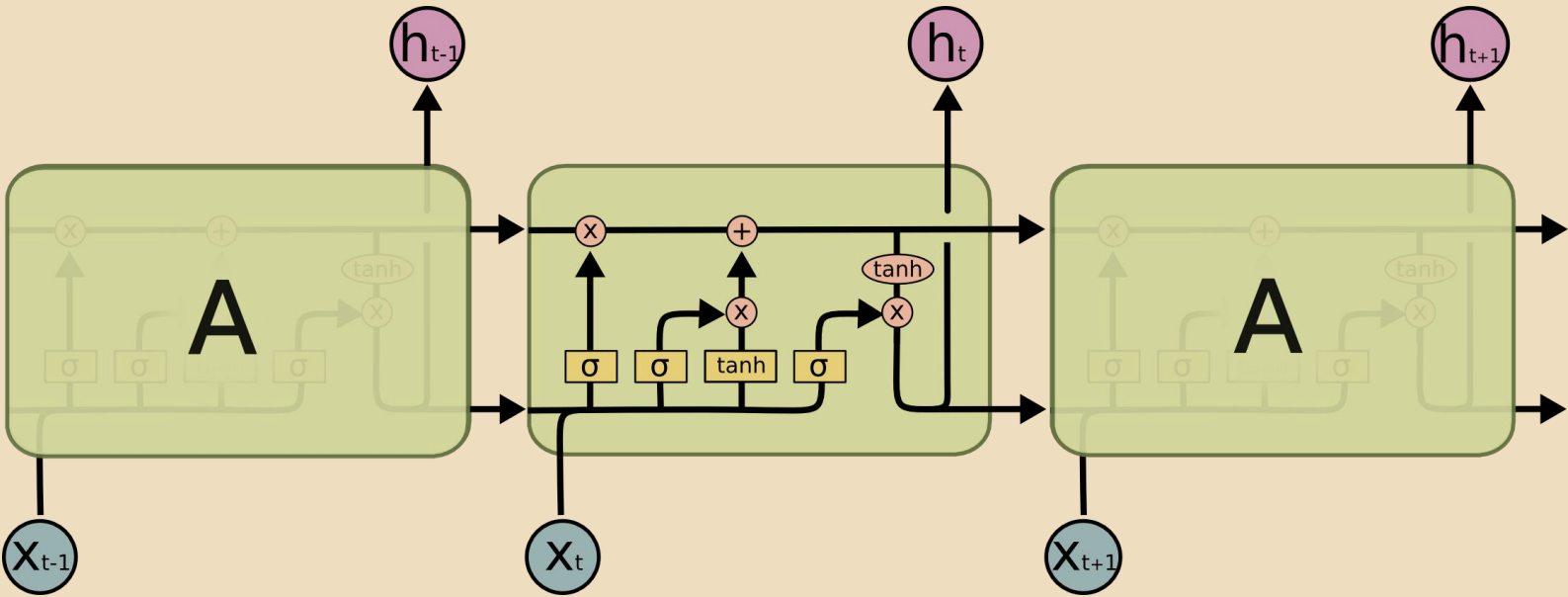
Attention

注意力机制（Attention）理论上能处理不受限制的序列长度，这意味着它能够灵活应对任意长度的序列数据。这是因为注意力机制在每个时间步都会进行信息聚合，而不受先前时刻的限制。只不过序列越长， 计算量越大。我们通常将attention所要处理的最大序列长度设置为在784。

Attention：是现阶段深度学习算法中一个非常重要的技能点，在很多领域中均可能使用到该技能点；直白来讲就是注意力机制，让模型学会在当前业务场景中需要关注那些特征信息，从而对这些需要关注的特征信息进行加强，常用的结构就是：Self-Attention结构。

image-20240504170636115

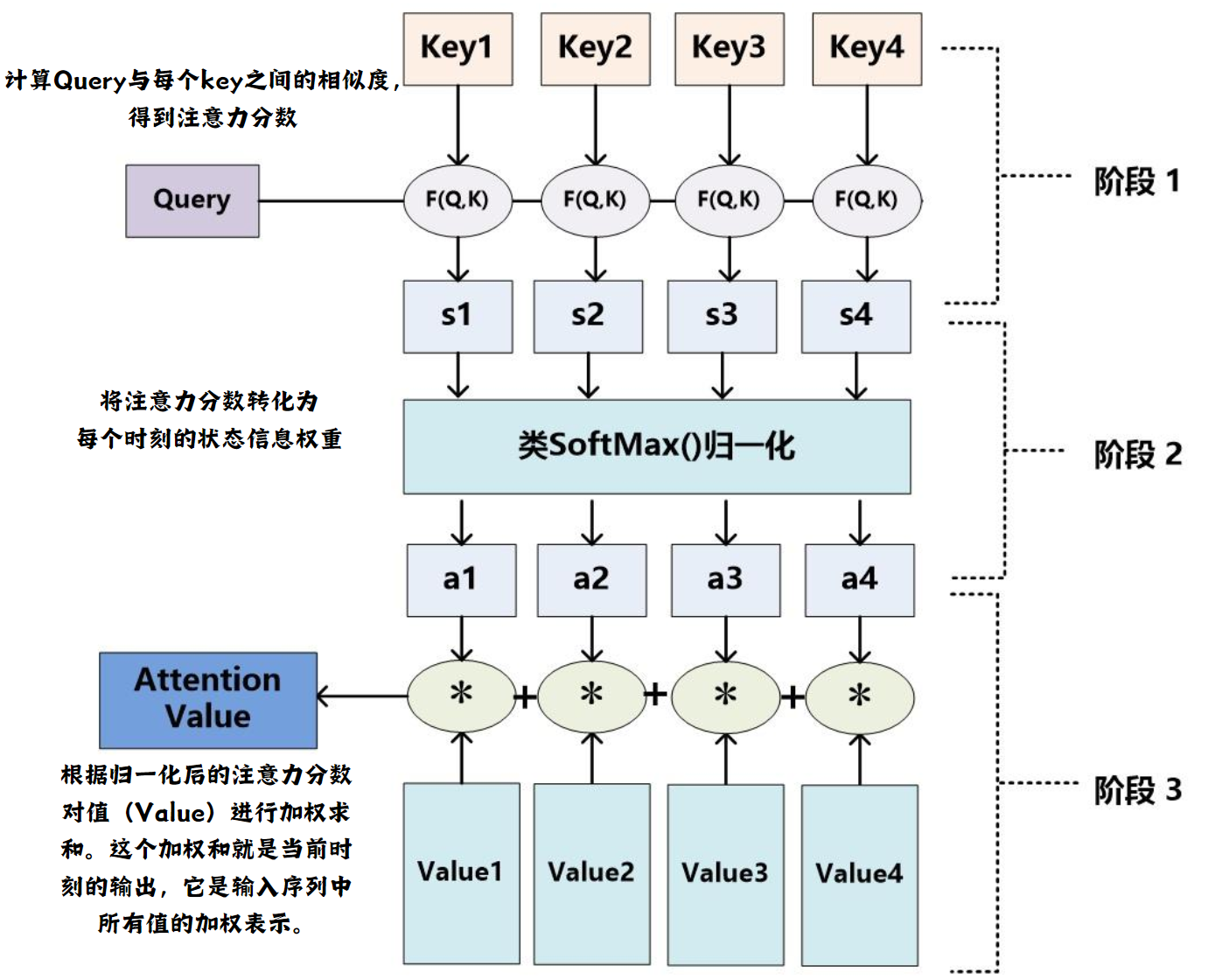
在Attention机制中，特别是在自注意力（Self-Attention）的实现中，每个时刻的Key、Query和Value通常是通过对每个时刻的输入向量进行不同的全连接（线性变换）操作得到的三个不同的向量， 即通过全连接每个时刻的输入进行特征提取。

具体来说，对于输入序列中的每个元素（或每个时刻的输入），我们使用三组不同的权重矩阵（通常是可学习的参数）来分别生成Query、Key和Value向量：

• Query向量是通过将输入向量与一个权重矩阵相乘（全连接操作）得到的，用于后续与Key向量进行匹配。
• Key向量也是通过将相同的输入向量与另一个权重矩阵相乘得到的，用于与Query向量进行匹配，以计算注意力分数。
• Value向量同样是通过将输入向量与第三个权重矩阵相乘得到的，一旦计算出注意力分数，这些Value向量将根据分数被加权求和，以生成最终的输出。

每个时刻的Query、Key、Value向量所对应的三个权重矩阵均相同（即Q1、K1、V1=...=Qn、Kn、Vn）， 但Query、Key、Value所对应的权重矩阵各不相同。

这种方法允许模型在处理每个输入元素时，能够考虑到整个序列的上下文信息，从而有效地捕捉序列内的长距离依赖关系。

image-20240504172436041

image-20240504165109224

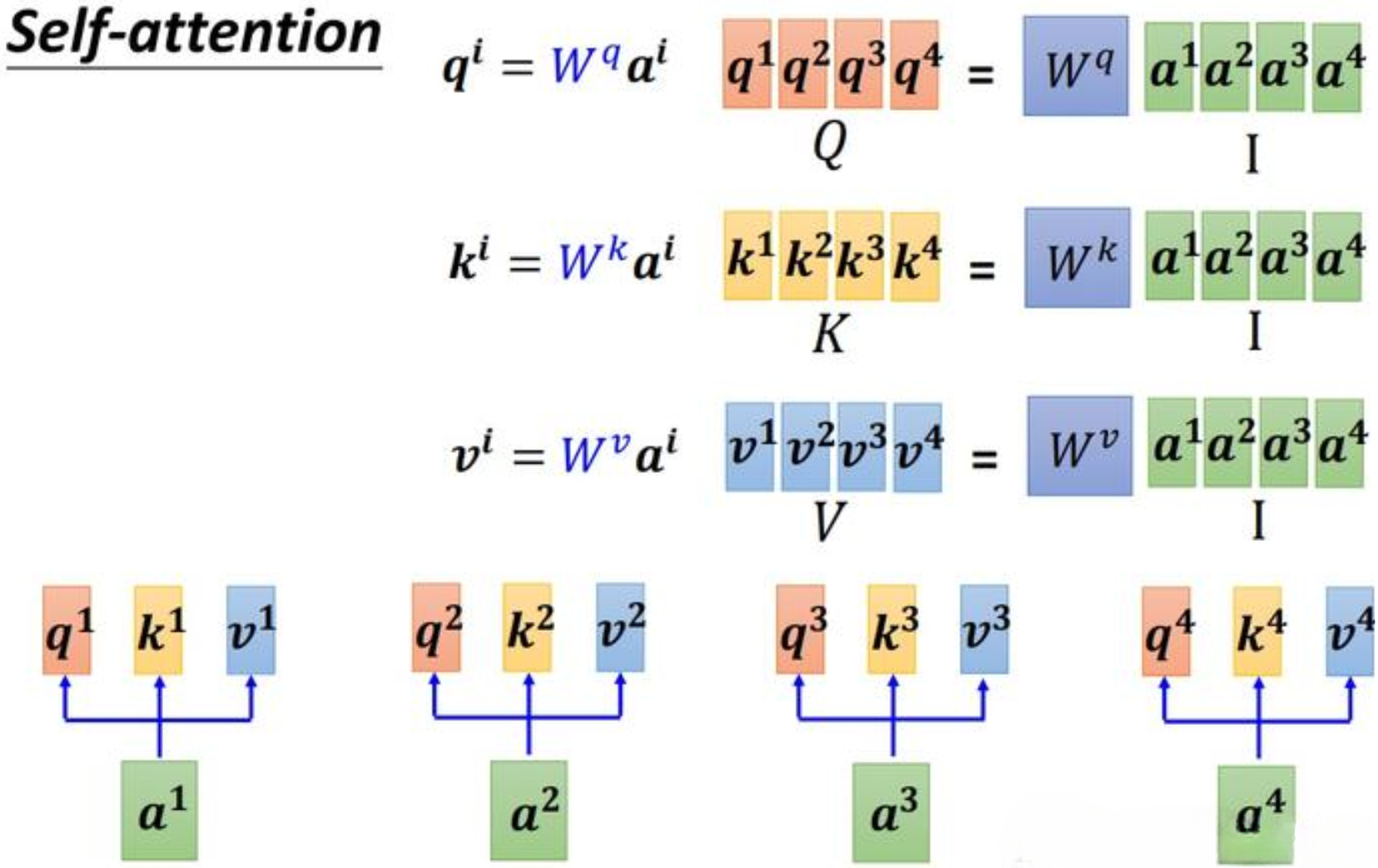
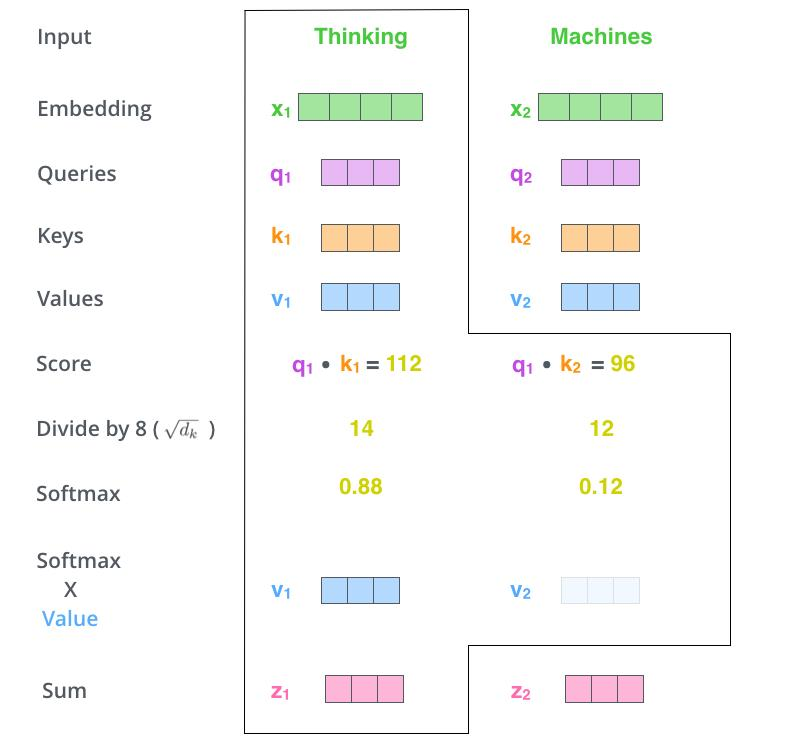
上述的过程简单来说就是\(Query\overset{计算与Key的相关性}{\rightarrow}\alpha \overset{softmax归一化得到权重系数}{\rightarrow}\beta \overset{与value相乘}{\rightarrow} z(当前时刻的特征信息)\)

查询（Query）、键（Key）和值（Value）这三个向量的来源可以是相同的，也可以是不同的。通常情况下，我们提到的Query、Key和Value可能源自同一输入时间步。然而，这些向量也可以有不同的来源。例如，一个Query可以是搜索引擎中的搜索词，而Key则可能对应一段文本或者商品的标识，Value则表示该商品的特征向量。在这里，Key和Value来源于相同的商品数据，而Query则来自不同的搜索词。关键在于，无论这些向量的来源如何，我们都将基于它们之间的相关性进行计算，接着以加权向量的形式进行特征信息表示。至于Query、Key和Value的具体来源，我们可以留有灵活性。特别地，当这些向量全部来自于同一实体时，这种模式被称为自注意力（self-attention）机制。

注意力机制（Attention Mechanism）的设计就是为了让模型能够自动学习到在给定的业务或任务环境中，哪些信息是更加重要的，因此应该被强化，而哪些信息是次要的，因此可以被减弱。这种机制使得模型能够更加聚焦于对结果影响最大的因素，从而提高模型处理信息的效率和效果。

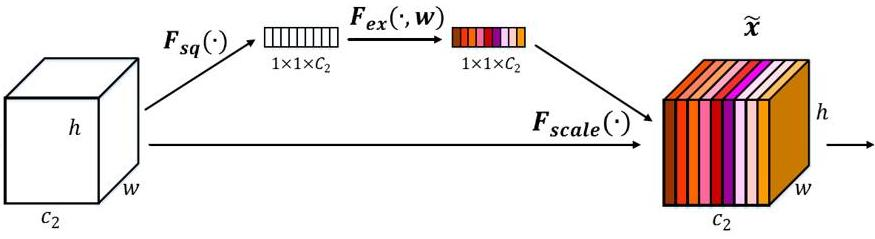
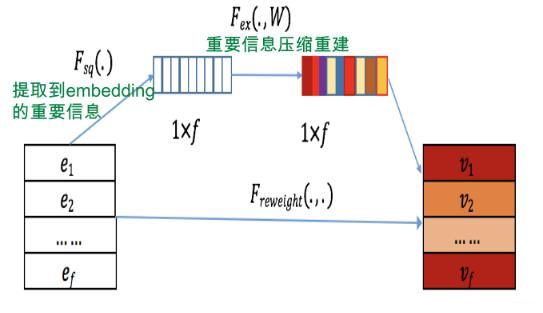
Attention：除了NLP基础里面介绍到的Attention之外，还有CV基础里面介绍的Attention也是非常重要的，比如:SENet中的通道Attention机制。

image-20240503160045696

image-20240503160057883

Attention vs RNN

Attention机制与RNN在计算当前时刻的特征信息时的主要区别在于：

1. 直接访问 vs. 顺序处理：
   • Attention：可以直接访问整个输入序列的任何部分，并根据当前的任务动态地聚焦于最相关的部分来计算当前时刻的输出。
   • RNN：必须顺序地处理输入序列，当前时刻的输出依赖于前一时刻的隐藏状态和当前的输入。
2. 全局上下文 vs. 局部信息：
   • Attention：为输入序列中的每个元素分配一个权重，从而在计算当前输出时考虑全局上下文。
   • RNN：每个时刻的输出主要受到局部前一时刻状态的影响，对于远距离的信息可能难以捕捉。
3. 并行计算 vs. 迭代计算：
   • Attention：所有时间步的计算可以并行进行，因为每个步骤的计算都是独立的。
   • RNN：必须迭代地计算每个时间步，因为每个步骤的输出依赖于前一个步骤的状态。

Attention机制通过直接关注输入序列中的相关部分来计算当前时刻的特征信息，而RNN则通过迭代地更新隐藏状态来进行计算，这使得Attention在处理长序列和并行计算方面更具优势。