Recommended system common algorithm
本章内容
项目:电影推荐系统
掌握算法:协同过滤算法、矩阵分解算法、LR、GBDT、FM、BPR、DSSM、YoutubeNet、DeepFM、xDeepFM等;
其它知识点:MySQL、Redis、Neo4j、Faiss、模型部署等;
最终提供一个HTTP的访问接口,接收请求参数(可能就是用户ID),产生一个推荐的商品列表;
数据集:MovieLens
MovieLens是一个专注于个性化电影推荐的项目,定义了在推荐系统中对数据的格式要求。在传统的协同过滤和矩阵分解思路的推荐系统框架中,基本上都要求数据格式必须是符合MovieLens定义的数据格式。其格式为:用户id、商品id、评分、时间戳(可选)。
\[ \begin{array}{|cccc|} \hline \text { userld } & \text { movield } & \text { rating } & \text { timestamp } \\ \hline 1 & 31 & 2.5 & 1260759144 \\ \hline 2 & 10 & 4.0 & 835355493 \\ \hline 3 & 84236 & 4.0 & 1298922130 \\ \hline \end{array} \]
Python推荐算法框架:Surprise
Surprise(Simple Python Recommendation System Engine)是scikit系列的一个库。支持多种推荐算法,是python语言使用实现推荐算法的首选方式。
- 官网:http://surpriselib.com/
- 文档:http://surprise.readthedocs.io/en/stable/
- 源码:https://github.com/NicolasHug/Surprise/
安装方式(依赖numpy服务):
- 推荐:conda install -c conda-forge scikit-surprise
- pip安装命令: pip install scikit-surprise
- 注意:如果用pip安装就一定需要安装c编译环境;
为什么我们使用pip安装surprise框架时需要c编译环境? 这主要是因为suprise中需要将c语言编写的.pyx文件(源码)编译成.c和.pyd文件。而这两个文件其实是和c相关的文件, 所以只有通过编译才能够直接进行使用。
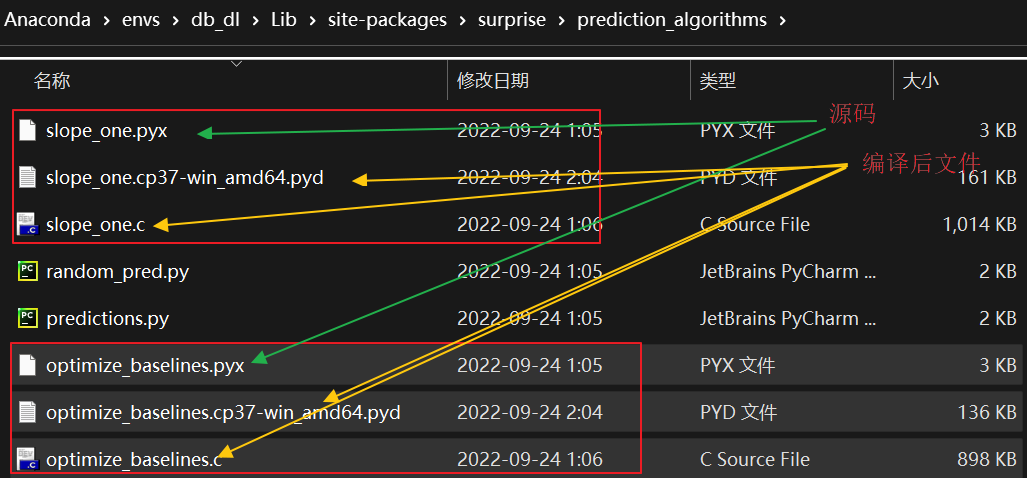
就拿suprise中的prediction_algorithms模块来说, 我们在pycharm中想查看prediction_algorithms模块中的baseline_sgd方法, 当我们打开后就是这样子
2
3
4
5
6
7
8
9
10
11def baseline_sgd(*args, **kwargs): # real signature unknown
"""
Optimize biases using SGD.
Args:
self: The algorithm that needs to compute baselines.
Returns:
A tuple ``(bu, bi)``, which are users and items baselines.
"""
pass这里说明这个方法底层是用 C 语言写的, 无法看到Python源代码
不过我们有时可以打开相应路径下的.pyx后缀的文件来查看某一用CPython编写的函数的源码: (注: CPython 是 Python 编程语言的 C 实现。 Cython 旨在成为 Python C 扩展。开发人员可以使用 Cython 来加速 Python 代码执行。)
在Python中,有些内置函数或方法的实现体只有一个
pass语句。这通常意味着它们是在Python的C实现层面(即CPython)中定义的。CPython是Python的官方解释器,它用C语言实现了Python的大部分标准库和内置功能。这样做有几个原因:
- 性能:用C语言编写的函数通常比纯Python代码执行得更快,因为它们可以直接与底层C API交互,减少了解释执行的开销。
- 接口一致性:Python提供了一致的接口,无论功能是用Python还是C实现的。这意味着从Python代码的角度来看,这些函数的行为和其他Python函数没有区别。
- 底层访问:有些操作需要访问Python解释器的底层细节,这些细节在Python层面是不可见的,但可以通过C语言访问。
当你在Python代码中看到一个只有
pass的函数或方法时,这通常是一个占位符,真正的实现在解释器的内部,不在Python层面的源代码中。这些函数和方法的定义通常在Python的C源代码中,它们被编译成二进制形式并内置在Python解释器中。例如,许多内置数据类型(如
list、dict)和它们的方法(如append()、get())都是用C语言实现的,以提供最佳性能。这些方法在Python层面看起来可能只有一个pass,但它们的实际功能是在编译后的CPython解释器中实现的。
2
3PyCharm做了一些相当出色的事情来提升开发者的使用体验。它会维护一个索引,这个索引中包含了当前解释器中所有的函数、类型等元素,从而支持开发者快速跳转到定义的位置。这是一个非常实用的功能。
至于内置函数,由于它们没有具体的实现可供IDE查找,PyCharm则采取使用Python文档(pydoc)来生成这些函数的签名。这些由PyCharm自动生成的签名,其函数体的内容通常为"pass",意味着该函数什么也不执行。这是一个巧妙的方法,不仅提供了丰富的内置函数信息,让开发者能更精确地理解和使用这些内置函数,同时也保障了IDE的运行效率。
Surprise支持基本的常用推荐算法:
- 基础算法/baseline algorithms
- 协同过滤算法(基于近邻算法)/neighborhood methods
- 矩阵分解算法/matrix factorization-based(SVD, SVD++, NMF)
\[ \begin{array}{0} \hline 算法 & 描述 \\ \hline \begin{array}{1} random\_pred.NormalPredictor \end{array} & 基于统计的随机预测打分,假定用户的打分分布是服从高斯分布的。 \\ \hline baseline\_only.BaselineOnly & 基于统计的基准线预测打分。 \\ \hline knns.KNNBasic & 基本的协同过滤算法。 \\ \hline knns.KNNWithMeans & 基本协同过滤算法的变种,考虑每个用户的平均评分。 \\ \hline knns.KNNWithZScore & 基本协同过滤算法的变种,考虑每个用户评分的归一化操作。 \\ \hline knns.KNNBaseline & 基本协同过滤算法的变种,考虑基于统计的基准线评分。 \\ \hline matrix\_factorization.SVD & SVD矩阵分解算法。 \\ \hline matrix\_factorization.SVDpp & SVD++矩阵分解算法。 \\ \hline matrix\_factorization.NMF & 一种基于非负矩阵分解的协同过滤算法。 \\ \hline slope\_one.SlopeOne & SlopeOne协同过滤算法。 \\ \hline co\_clustering.CoClustering & 一种基于协同聚类的协同过滤算法。 \\ \hline \end{array} \]
http://surprise.readthedocs.io/en/stable/prediction_algorithms_package.html
| 相似度度量标准 | 描述 |
|---|---|
| cosine | 计算所有用户或者所有物品之间的余弦相似度。 |
| msd | 计算所有用户或者所有物品之间的平均平方差相似度。 |
| pearson | 计算所有用户或者所有物品之间的皮尔森相似度。 |
| pearson_baseline | 使用基准线方式计算皮尔森相似度。 |
http://surprise.readthedocs.io/en/stable/similarities.html
| 评估准则 | 描述 |
|---|---|
| rmse | Root Mean Squared Error, 计算均方根误差。 |
| mae | Mean Absolute Error, 计算平均绝对误差。 |
| fcps | Fraction of Concordant Pairs. |
http://surprise.readthedocs.io/en/stable/accuracy.html
推荐算法_ Normal Predictor
Normal Predictor是一种假定用户对物品的评分数据是服从正态分布的, 从而可以基于正态分布的期望 \(\mu\) 和标准差。随机的给出当前用户对于其它物品的评分。 基于大数定理或者使用最大似然估计(MLE)我们可以得到每个用户评分数据所属正态分布对应的期望 \(\mu\) 和标准差 \(\sigma\) 分别为: \[ \begin{gathered} \mu=\frac{1}{\left|R_{\text {train }}\right|} \sum_{r_{u i} \in R_{\text {train }}} r_{u i} \quad \sigma^2=\frac{1}{\left|R_{\text {train }}\right|} \sum_{r_{u i} \in R_{\text {train }}}\left(r_{u i}-\mu\right)^2 \\ f\left(r_{u i}\right)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(r_{u i}-\mu\right)^2}{2 \sigma^2}} \end{gathered} \]
在 "NormalPredictor" 算法中,评分的预测通常由下面的步骤构成:
- 确定参数:通过分析历史评分数据来确定正态分布的参数,即均值 和标准差 。
- 随机预测:使用这些参数,为每个用户-物品对生成一个预测评分,这个评分是从以 为均值, 为标准差的正态分布中随机抽取的。
- 概率密度函数:在某些情况下,"NormalPredictor" 可能会使用正态分布的概率密度函数来估计用户可能给出的评分值的概率密度。
"NormalPredictor" 通常不是最精确的推荐算法,因为它依赖于随机性,而且没有考虑用户或物品的特定特征。然而,它可以作为一个基线(baseline)模型,用于比较其他更复杂的算法的性能。在没有足够的用户或物品特征信息的情况下,或者在初步构建推荐系统时,"NormalPredictor" 可以提供一个起点。此外,在某些情况下,如果用户的评分行为确实接近正态分布,这种方法可能会给出合理的预测结果。
推荐算法_Baseline Only
基线(Baseline)的含义其实是相对于平均值的偏差。假定现在需要使用Baseline Only算法给出gerry对于《缩小人生》这部电影的评分。比如我们现在计算出所有电影的评分均值为3.7分。此外,《缩小人生》这部电影由于属于喜剧科幻类型的电影,所以它的平均评分比其他电影评分低0.3分。在另一方面,gerry用户是一个要求比较宽松的用户,通常会比别人多给0.8个评分。因此,我们最终可以计算出gerry用户对于《缩小人生》这部电影的评分为:3.7 - 0.3 + 0.8 = 4.2分。
Baseline Only是一种基于统计数据的基线评分预测算法。其原理是认为每个用户对于每个商品的评分是由三部分构成的,即所有用户对所有物品的评分的均值μ(全局平均评分:全局总体评分(通常表示为 μ)指的是在推荐系统的数据集中,所有用户对所有物品的评分的均值。简而言之,它是所有评分的平均值,不区分不同的用户或物品。这个值提供了一个基本的参考,表明了整个数据集中评分的一般水平。在计算用户对某个物品的预测评分时,全局平均评分是一个重要的基线,可以在此基础上进一步考虑用户偏差和物品偏差。)
当前用户的评分基线bu(用户偏差:当前用户的所有评分与全局平均评分的差的平均值,代表了该用户相对于其他用户的评分倾向。)、
当前物品的评分基线bi(物品接收的评分相对于全局平均评分的偏差)。即评分公式如下:
\[ \begin{align} \hat{r}_{ui} = b_{ui} = \mu + b_u + b_i \\ \text{如果我们选用的损失优化方式是 ALS, 那么我们可以为} \lambda_u \text{和} \lambda_i \text{分别指定不同的正则化参数:} \\ J(b_u, b_i) = \sum_{r_{ui} \in R_{\text{train}}} \left( r_{ui} - \mu - b_u - b_i \right)^2 + \lambda_u \sum_u b_u^2 + \lambda_i \sum_i b_i^2 \\ \quad b_u, b_i = \min_{b_*} J(b_u, b_i) \\ \text{如果我们选用的损失优化方式是 SGD 的话, 那么正则化项的权重系数是统一设置的,即:} \\ J(b_u, b_i) = \sum_{r_{ui} \in R_{\text{train}}} \left( r_{ui} - \mu - b_u - b_i \right)^2 + \lambda \left( \sum_u b_u^2 + \sum_i b_i^2 \right) \\ & \quad b_u, b_i = \min_{b_*} J(b_u, b_i) \end{align} \]
\(b_{u i}\)待求的基线模型中用户u给物品i打分的预估值
\(b_u:\) user偏差 (如果用户比较苛刻,打分都相对偏低,则bu<0;反之,bu>0) ;
\(b_i:\) item偏差,反映商品受欢迎程度
推荐算法_协同过滤
协同过滤(CF,Collaborative Filtering),也叫做基于近邻的推荐算法,其主要思想是利用已有的用户群过去的行为或者意见来预测数据, 简单来说, “协同过滤”就是协同⼤家的反馈、评价和意见⼀起对海量的信息进⾏过滤,从中筛选出⽬标⽤户可能感兴趣的信息的推荐 过程。它根据和当前用户/当前物品比较相似的近邻数据来产生推荐结果,类似于KNN算法的思想,是一种非常基础、非常常用的经典推荐算法。
该算法的输入是一个用户-物品评分矩阵,输出的数据一般有两类:当前用户对物品喜欢和不喜欢程度的预测评分数值以及N项推荐物品的列表。
协同过滤算法的优势:
简单性:实现简单,而且在调整参数的过程中只有一个近邻数需要调整。
合理性:对于预测推荐提供了简洁并直观的理由。
高效性:基于近邻方法的推荐的效果特别高,因为可以先进行预处理,构建出相似度矩阵。在实际应用过程中,可以提供近似实时的推荐结果。
稳定性(ItemCF):当相似度矩阵构建完成后,如果有用户对物品产生新的评分,那么影响的范围是很小的。
由于在CF算法中,需要输入的是用户-物品评分矩阵,所以构建用户-物品评分矩阵是一个在进行协同过滤的重点。评分一般采用两分制、五分制、七分制和十分制这四种。CF算法基于的数据是用户-物品评分矩阵, 所以说我们的数据中需要包含物品的评分, 但评分其实很难收集, 而评分不好收集,就会导致模型不好学习。于是数据的评分就分为两种形式, 我们可以通过以下两种方式收集用户对物品的评分,分别是:
- 显式评分:通过问卷调查的方式收集用户对于商品的评分。优点是数据比较准确,缺点是当用户看不到好处的时候可能不会提供评分。
显式评分, 其实就是让用户主动评,但是让用户主动评,存在着一个问题, 比如说点外卖,我相信我们都不怎么会进行评分吧,但外卖单子上经常会有好评返现, 于是乎, 就会存在一个问题,就是这个评分的可信度相对来讲就不好说, 就是如果说在理论情况下, 也就是没有外界干扰的情况下,用户主动评的评分才能够体现用户的本质需求,但是,由于评分经常会有外界因素影响,而最主要原因也就是用户不怎么去评分。
当然了,实际上,哪怕存在好评返现的情况,我们仍然认为这种数据是还可以的。为什么呢?因为,至少在某些情况下,比如说外卖,用户给出好评是基于一定的前提条件的。那就是,食物的味道至少是可接受的, 在这种情况下, 好评返现可能会吸引用户给出好评。或者说当食物的味道非常不错的时候,用户也会给出好评。但如果食物的味道实在是太差,即便有好评返现的诱惑,用户也可能会选择给出差评。
- 隐式评分:当用户购买一个商品或者浏览一个商品的时候,我们可以认为这是一个正向评分/正向意图。根据既定的规则,可以将其转换为评分值。这种方式的优点是可以收集到较多的数据,缺点是很难保证得到的评分数据是一个准确的用户评分数据。
不管如何操作,实际上用户物品评分矩阵基本上都是一个非常稀疏的矩阵,也就是只有少量用户在少量商品上有评分。这种情况会直接导致模型效果变差;这种情况有一个通用的名称,叫做冷启动问题。冷启动问题在推荐领域中主要包括以下两种情况:
- 如果向还没有任何交互行为的新用户产生推荐列表?
- 如果将新商品推送给用户?
解决方案:
- 利用混合方法进行推荐,采用多种机器学习、深度学习模型完成推荐。
- 采用ItemCF算法(变种)中的相似度矩阵的策略来缓解冷启动(实际上就是采用I2I策略推荐)。
- 利用新品推荐强制将新商品推送给用户。
- 利用热门推荐给新用户推送商品列表。
计算新商品和其他商品的相似度:
在推荐系统中,对于新商品(通常称为冷启动物品),计算其与其他商品之间的相似度是一个挑战,因为新商品缺乏用户的交互数据。为了解决这个问题,可以采用以下一些方法来计算新商品与其他商品之间的相似度:
1. 基于内容的相似度计算
- 文本信息:利用商品的描述、标题、关键词等文本信息,通过自然语言处理技术(如TF-IDF、Word2Vec、BERT等)提取特征,然后计算新商品与现有商品之间的文本相似度。
- 视觉信息:如果商品有图片,可以使用图像处理技术(如CNN)提取图像特征,然后计算新商品与现有商品之间的视觉相似度。
- 属性信息:基于商品的属性信息(如品牌、类别、价格等)计算相似度。这可能涉及到将这些属性转换为数值特征,然后使用余弦相似度、欧氏距离等方法计算相似度。
2. 基于协同的方法
即使是新商品,也可能在一开始就有少量的用户交互数据(如点击、收藏等)。可以利用这些初步数据结合协同过滤技术,通过用户对其他商品的评分或交互,间接计算新商品与其他商品的相似度。
3. 混合方法
- 基于模型的方法:使用包含内容信息和用户交互的混合推荐模型,如因子分解机(Factorization Machines),可以同时考虑商品内容特征和用户行为数据,对新商品进行有效的相似度计算。
- 多模态学习:如果商品具有多种类型的信息(如文本、图像等),可以采用多模态学习方法整合这些信息,提高相似度计算的准确性。
4. 社交网络信息
如果推荐系统可以访问社交网络数据,可以利用用户在社交网络上的行为和关系,通过分析用户群体对新商品的态度和反应,间接推断新商品与其他商品的相似度。
采用这些方法时,关键在于如何有效地整合多种信息源和技术,以克服新商品缺乏历史交互数据的问题,从而准确地计算出新商品与其他商品之间的相似度,提高推荐系统的性能。
基于近邻的算法是基于评分之间的关联性进行推荐的,所以存在两个重要的缺陷:
- 覆盖有限:由于计算两个用户之间的相似性是基于他们对相同物品的评分,而且只有对相同物品进行评分的用户才能作为近邻。然而,在实际应用中,有些用户有很少或者没有共同评分,但是他们可能具有相似的爱好,因此推荐算法的覆盖将会受到影响。
- 对稀疏数据的敏感:由于用户只会对一部分物品进行评分,所以评分矩阵的稀疏性是大多数推荐系统的共同问题。当数据是稀疏的时候,两个用户或者物品之间的相似性计算仅适用很少量有限的近邻。另外,相似性权重的计算也可能依赖小部分评分,从而有可能导致推荐偏差。这也是一个比较重要的问题:冷启动问题。
主要/最基础的实现方式包括:
- 基于用户的最近邻推荐(UserCF)
- 基于物品的最近邻推荐(ItemCF)
简单来说:
- UserCF(基于用户的协同过滤):这种方法首先找到与目标用户最相似的K个用户(即“邻居”),然后根据这些相似用户对特定物品的评分来预测目标用户对该物品的评分。这种方法的核心思想是,相似的用户可能对物品有类似的评价。
- ItemCF(基于物品的协同过滤):这种方法首先识别出目标用户已经评价过的物品,然后找到这些物品与其他物品之间的相似度。接着,基于这些相似度以及用户对已评价物品的评分,来预测用户对未评价物品的评分。这种方法的核心思想是,用户可能会对相似的物品给出相似的评分。
两种方法各有优势,UserCF侧重于利用用户之间的相似性来进行推荐,而ItemCF侧重于物品之间的相似性。在实际应用中,选择哪种方法取决于具体的业务场景和数据特性。例如,如果物品的数量远小于用户的数量,ItemCF可能会更有效,因为计算物品之间的相似度比计算用户之间的相似度更容易管理。相反,如果用户的行为模式比较稳定,UserCF可能会提供更准确的推荐。
UserCF在计算相似度的过程中是多用户单商品, 而ItemCF在计算相似度的过程中是单用户多商品。具体来说就是UserCF是通过多个相似用户对指定商品的评分然后加权计算用户对某一商品的评价, ItemCF是基于当前用户评价过的其他商品的评分然后加权计算用户对某一商品的评分。
在使用UserCF时我们更常用的计算相似度的指标是皮尔逊相关系数, 因为皮尔逊相关系数更多的考虑评分的趋势而不是绝对值。这对于比较用户的评分行为特别有用,因为即使两个用户的评分标准不同(例如,一个用户评分较严格,另一个评分较宽松),但他们可能仍然对物品有相似的喜好和评分趋势。那么在这种情况下,我们通过趋势来判断用户间的相似度可能就会更加的好一些。而在使用ItemCF时我们更常用的计算相似度的指标则是余弦相似度。余弦相似度通过比较两个物品评分向量的夹角来计算相似度,它只关注评分向量的方向而不是大小,这意味着它只考虑了用户评分模式的一致性,而不受用户评分量值的影响。这在物品间的相似度计算中是有意义的,因为我们更关心的是哪些物品被相似的用户群体评分,而不是具体的评分值。
\[ \begin{array}{|c|c|c|} \hline & \text { UserCF } & \text { ItemCF } \\ \hline \text { 性能 } & \begin{array}{l} \text { 适用于用户较少的场合, 如果用户过 } \\ \text { 多, 计算用户的相似度矩阵代价比较 } \\ \text { 高。 } \end{array} & \begin{array}{l} \text { 适用于物品数明显小于用户数的场合, 如 } \\ \text { 果物品数过多, 计算物品之间的相似度矩 } \\ \text { 阵代价过大。 } \end{array} \\ \hline \text { 领域 } & \begin{array}{l} \text { 时效性较强, 用户个性化兴趣不明显 } \\ \text { 的领域(可在一定程度上帮助拓展用户的兴趣面) } \end{array} & \begin{array}{l} \text { 长尾物品丰富, 用户个性化需求强烈的领 } \\ \text { 域 } \end{array} \\ \hline \text { 实时性 } & \begin{array}{l} \text { 用户有新行为, 不一定会对推荐结果 } \\ \text { 产生影响 } \end{array} & \begin{array}{l} \text { 用户有新行为的时候, 一定会导致推荐结 } \\ \text { 果实时变化 } \end{array} \\ \hline \text { 冷启动 } & \begin{array}{l} \text { 在新用户对很少物品产生行为的时候, } \\ \text { 不能立即对用户进行个性化推荐 } \\ \text { 新物品上线一段时间后,一旦有用户 } \\ \text { 对该物品产生行为, 那么就可以将新 } \\ \text { 物品推存给其他兴趣相似的用户 } \end{array} & \begin{array}{l} \text { 新用户只要对一个物品产生行为, 就可以 } \\ \text { 给他推在和该物品相似的其它物品 } \\ \text { 必须等到更新物品相似度矩阵的时候才可 } \\ \text { 以将新物品更新进去。 } \end{array} \\ \hline \text { 推荐理由 } & \begin{array}{l} \text { 很难提供令用户信服的推荐解释 }\\ \text { (比如某用户喜欢喜剧,}\\ \text { 然后因为另一喜欢喜剧又喜欢战争的相似用户}\\ \text { 于是突然推了一个战争片)} \end{array} & \begin{array}{l} \text { 利用用户的历史行为做推荐解释, 可以令 } \\ \text { 用户比较信服 } \end{array} \\ \hline \end{array} \]
协同过滤算法在整个体系中的定位就是召回
UserCF
其实在suprise框架中最重要的算法就是协同过滤算法
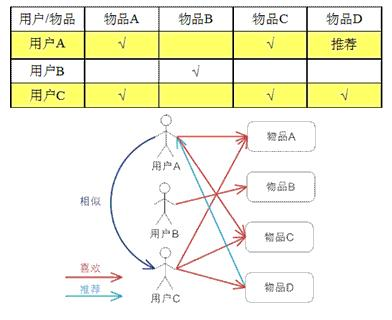
基于用户的最近邻推荐(User-based Nearest Neighbor Recommendation,UserCF)的主要思想包括以下步骤:
说白了就是把相似用户喜好的商品作为当前用户的一个推荐列表,本质上就是选则相似用户并把相似用户喜好的商品作为当前用户的推荐。
- 针对输入的评分数据集和当前用户ID,找出与当前用户过去有相似偏好的其他用户,这些用户被称为对等用户或者最近邻。
- 对于当前用户没有见过的每个产品p,利用用户的近邻对产品p的评分进行预测。
- 选择所有产品评分最高的TopN个产品推荐给当前用户。
UserCF的主要前提/假设包括:
当我们根据计算得来的当前用户和其他用户的相似度后, 并找到相似用户之后, 然后我们现在把这些相似用户所喜好的商品p的评分做一个加权融合,这样就会产生当前用户对于商品p的评分, 然后不断遍历即可达到这个效果。简单来说就是物以类聚人以群分的思路。
- "物以类聚人以群分"中人以群分的思想:如果两个用户共同喜好的商品越多,即这两个用户更加相似,那么这两个用户就有非常高的可能喜欢对方喜欢的商品。
- 用户的偏好不会随时间发生变化。
首先,我们计算各个用户之间的相似度。在分析后,我们发现某用户与小松鼠的相似度异常高。因此,我们决定将小松鼠喜爱的物品推荐给该用户。这一决策的依据是历史数据显示这两位用户的行为习惯极为相似。
那么,我们是如何进行这项操作的呢?首先,我们计算所有用户之间的相似度矩阵。这就是我们执行推荐过程的基础。

UserCF算法执行流程如下:
计算所有用户与用户之间的相似度矩阵(基于用户共同评价商品列表来计算相似度)
计算当前用户u对于当前物品i的评分方式如下: 2.1. 获取和当前用户u最相似的K个近邻用户(要求这K个近邻用户在物品i上有评分)。
在surprise框架中, 我们是通过ir(结构:{item: [user, rating]})来找到在物品i上进行评分的每一个用户, 然后对当前用户计算与物品i所对应的每一个用户的相似性, 即可得出k个在物品i上有评分的近邻用户。如此一来我们不需要遍历所有的用户求相似度, 大大提高了效率。
2.2. 根据K个近邻用户对物品i的评分计算当前用户对物品i的评分。
重复步骤2,计算出当前用户对所有物品的评分。
重复步骤2和3,计算所有用户对所有物品的评分。
对于每个用户,提取该用户对所有物品的评分排序后,评分最高的N个商品作为推荐商品列表。
注意:在提取推荐商品列表的时候,可以考虑将用户已访问商品去除。
1 | |
协同工具其实是拿着两个用户同时评价过的商品序列,然后基于这两个用户在这些有交集的商品序列的评分来计算用户间的相似度。并且影响用户间相似度的实际上是用户所共同评价过的商品的列表, 如果共同评价过的商品列表越长, 那计算出的用户间的相似度或者可信度就足够的高。
最原始的UserCF:首先获取出 K个最相似的近邻用户,然后将这些用户对物品 的评分进行加权求和。 \[ \hat{r}_{u i}=\frac{\sum_{v \in N_i^k(u)} \operatorname{sim}(u, v) * r_{v i}}{\sum_{v \in N_i^k(u)} \operatorname{sim}(u, v)} \] $ N_i^k(u)$\(\begin{aligned}\text{ 是对物品 }i\text{ 评分的用户中与用户 }u\text{ 相似度最高的前 }k\text{ 个用}\text{户的集合。}\end{aligned}\)
进行均值转换后的UserCF:该算法的原理是认为用户对物品的评分应该是位于该用户对所有物品评分的均值附近的,
所以在计算过程中, 不是直接使用相似用户对物品的评分,
而是使用物品评分和期望之间的差值进行计算。 \[
\hat{r}_{u i}=\bar{r}_u+\frac{\sum_{v \in N_i^k(u)}
\operatorname{sim}(u, v) *\left(r_{v i}-\bar{r}_v\right)}{\sum_{v \in
N_i^k(u)} \operatorname{sim}(u, v)}
\] 在进行基线转换后的UserCF算法中,
使用baseline的值来代替均值即可。因为均值体现的是当前用户在所有物品中的评分均值,
而baseline可以认为是当前用户在当前物品上可能的评分,
通过计算相似用户实际评分和baseline可能评分之间的差值从而可以得到当前用户的预测评分(预测评分
\(=\) baseline + 可能的差值) \[
\hat{r}_{u i}=b_{u i}+\frac{\sum_{v \in N_i^k(u)} \operatorname{sim}(u,
v) *\left(r_{v i}-b_{v i}\right)}{\sum_{v \in N_i^k(u)}
\operatorname{sim}(u, v)}
\] 基于评分数据矩阵采用UserCF预测gerry用户对于物品5的评分 \[
\begin{array}{|c|c|c|c|c|c|c|}
\hline & \text { 物品1 } & \text { 物品2 } & \text { 物品3 }
& \text { 物品4 } & \text { 物品 5 } & \text { 均值 } \\
\hline \text { Gerry } & 5 & 3 & 4 & 4 & ? & 4
\\
\hline \text { 用户1 } & 3 & 1 & 2 & 3 & 3 & 2.4
\\
\hline \text { 用户2 } & 4 & 3 & 4 & 3 & 5 & 3.8
\\
\hline \text { 用户3 } & 3 & 3 & 3 & 5 & 4 & 3.6
\\
\hline \text { 用户4 } & 1 & 5 & 5 & 2 & 1 & 2.8
\\
\hline
\end{array}
\] 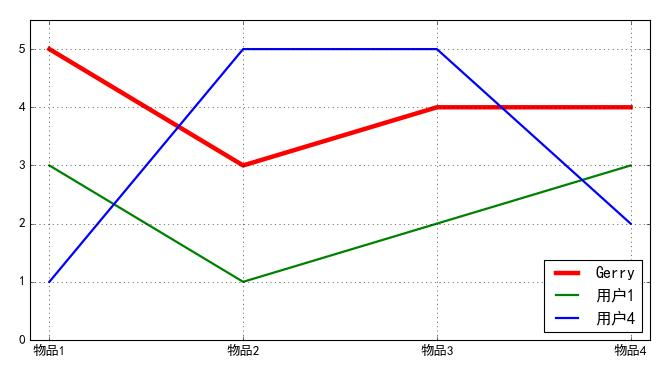
皮尔逊相关系数计算两个变量的相似度时, 实际上比较的就是两个变量的变化趋势。
用户Gerry和其它用户之间的相似度列表 \[ per\_sim_{u,\nu}=\frac{\sum_{i\in I_{u,\nu}}\left(r_{u,i}-\overline{r}_{u}\right)\left(r_{\nu,i}-\overline{r}_{\nu}\right)}{\sqrt{\sum_{i\in I_{u,\nu}}\left(r_{u,i}-\overline{r}_{u}\right)^2}\sqrt{\sum_{i\in I_{u,\nu}}\left(r_{\nu,i}-\overline{r}_{\nu}\right)^2}} \]
\[ \begin{array}{|l|l|l|l|l|} \hline & \text { 用户1 } & \text { 用户2 } & \text { 用户3 } & \text { 用户4 } \\ \hline \text { Gerry } & 0.853 & 0.707 & 0.0 & -0.792 \\ \hline \end{array} \]
选择 \(K\) 为 2 , 那么可以得到Gerry对物品 5 的评分预测为: 4.872 \[ \operatorname{pred}(\text { gerry, product } 5)=4+\frac{0.853 *(3-2.4)+0.707 *(5-3.8)}{0.853+0.707}=4.872 \]
ItemCF
基于物品的最近邻推荐(Item-based Nearest Neighbor Recommendation,ItemCF)的思想是基于物品之间的相似度来进行预测评分值,而不是基于用户之间的相似度。与UserCF相比,ItemCF有一个主要区别点:UserCF计算的是用户之间的相似度,从而将相似用户喜好的物品推荐给当前用户;而ItemCF中计算的是物品与物品之间的相似度,从而根据当前用户喜好的物品来推荐其他物品列表。
ItemCF的主要前提/假设包括:
- "物以类聚,人以群分"中物以类聚的思想。如果两个商品同时被多个用户偏好,那么表示这两个商品具有非常高的相似度,针对只浏览过单一商品的用户就可以推送另外一个商品作为偏好商品。
- 用户的偏好不会随时间发生变化。
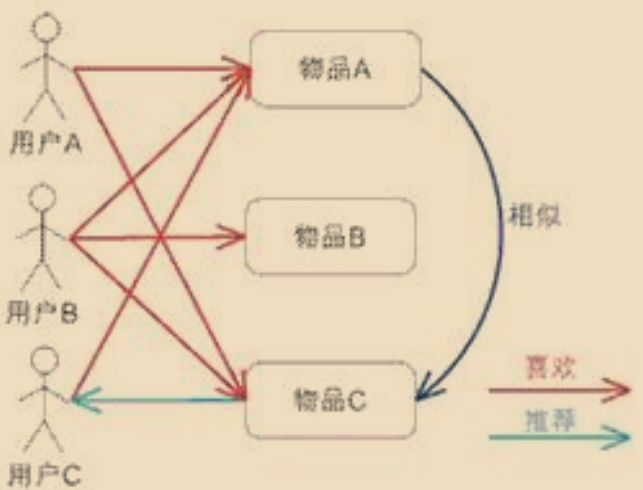
ItemCF算法执行流程如下:
- 计算所有商品与商品之间的相似度矩阵(基于两个商品共同被用户评论的共同用户列表)
- 计算当前用户u对于当前物品i的评分方式如下: 2.1. 获取和当前物品i最相似的K个近邻物品(要求这K个近邻物品都被用户u评分过)。 2.2. 根据用户u对K个近邻物品的评分计算当前用户对物品i的评分。
- 重复步骤2,计算出当前用户对所有物品的评分。
- 重复步骤2和3,计算所有用户对所有物品的评分(用户物品评分矩阵)。
- 对于每个用户,提取该用户对所有物品的评分排序后,评分最高的N个商品作为推荐商品列表。
注意:在提取推荐商品列表的时候,可以考虑将用户已访问商品去除。
最原始的ItemCF:首先获取出 \(\mathrm{K}\) 个最相似的近邻物品, 然后将当前用户在这些物品上的评分进行加权求和。 \[ \hat{r}_{u i}=\frac{\sum_{j \in N_u^k(i)} \operatorname{sim}(i, j) * r_{u j}}{\sum_{j \in N_u^k(i)} \operatorname{sim}(i, j)} \] 进行均值转换后的ItemCF:该算法的原理是认为用户u对物品i的评分应该是位于该物品 i \(^2\) 其它所有用户评分的均值附近的。所以在计算过程中, 不是直接使用用户u对相似物品的评分, 而是使用物品评分和期望之间的差值进行计算。 \[ \hat{r}_{u i}=\bar{r}_i+\frac{\sum_{j \in N_u^k(i)} \operatorname{sim}(i, j) *\left(r_{u j}-\bar{r}_j\right)}{\sum_{j \in N_u^k(i)} \operatorname{sim}(i, j)} \] 在进行基线转换后的ItemCF算法中,使用baseline的值来代替均值即可。因为均值体现的是所有用户在当前物品 \(i\) 中的评分均值, 而baseline可以认为是当前用户u在当前物品i上可能的评分,通过计算用户 \(u\) 在相似物品 \(\mathrm{L}\) 上的实际评分和baseline可能评分之间的差值从而可以得到用户 \(u\) 的对于物品i预测评分(预测评分=baseline + 可能的差值) \[ \hat{r}_{u i}=b_{u i}+\frac{\sum_{j \in N_u^k(i)} \operatorname{sim}(i, j) *\left(r_{u j}-b_{u j}\right)}{\sum_{j \in N_u^k(i)} \operatorname{sim}(i, j)} \]
我们可以这么理解, 就是结合所有用户对所有商品的总体平均评分+用户的偏好+商品的受欢迎程度来估计出一个大致的评分, 最后再基于用户对相似商品的实际评分和baseline评分之间的差值即可计算出用户对指定商品的评分。 举个例子, 比如用户喜欢看变形金刚系列的电影, 并且经常打高分,假如现在新出了一部变形金刚的电影, 我们在所有用户对所有电影的总体平均评分之上, 结合用户的偏好习惯以及电影的受欢迎程度即可预估出该用户对这部新上映电影的大致评分,最后再结合用户对相似电影的实际评分与baseline之间的差值即可预测出该用户对这部新上映的电影的评价。
基于评分数据矩阵采用ItemCF预测gerry用户对于物品5的评分 \[
\begin{array}{c|c|c|c|c|c|}
\hline & \text { 物品1 } & \text { 物品2 } & \text { 物品3 }
& \text { 物品4 } & \text { 物品5 } \\
\hline \text { Gerry } & 5 & 3 & 4 & 4 & ? \\
\hline \text { 用户1 } & 3 & 1 & 2 & 3 & 3 \\
\hline \text { 用户2 } & 4 & 3 & 4 & 3 & 5 \\
\hline \text { 用户3 } & 3 & 3 & 3 & 5 & 4 \\
\hline \text { 用户4 } & 1 & 5 & 2 & 4 & 1 \\
\hline \text { 均值 } & 3.2 & 3.0 & 3.0 & 3.8 & 3.25
\\
\hline
\end{array}
\] 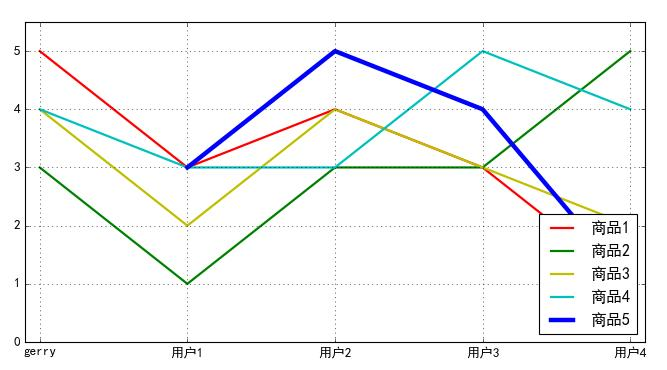
物品5和Gerry评价过的其它物品之间的相似度列表 \[ per\_sim_{i,j}=\frac{\sum_{u\in U_{i,j}}\left(r_{u,i}-\overline{r_i}\right)\left(r_{u,j}-\overline{r_j}\right)}{\sqrt{\sum_{u\in U_{u,\nu}}\left(r_{u,i}-\overline{r}_i\right)^2}\sqrt{\sum_{u\in U_{u,\nu}}\left(r_{u,j}-\overline{r}_j\right)^2}} \]
\[ \begin{array}{|c|c|c|c|} \hline & \text { 物品1 } & \text { 物品2 } & \text { 物品3 } & \text { 物品4 }\\ \hline \text { 物品5 } & 0.969 & -0.478 & 0.866 &-0.153\\ \hline \end{array} \]
选择 \(K\) 为 2 , 那么可以得到Gerry对物品 5 的评分预测为:4.672 \[ \operatorname{pred}(\text { gerry, product } 5)=3.25+\frac{0.969 *(5-3.2)+0.866 *(4-3.0)}{0.969+0.866}=4.672 \] ItemCF变种
基于物品的最近邻推荐可以离线进行数据预计算。首先构建一个物品相似度矩阵,用于描述两个物品之间的相似度,然后针对每个物品提取最相似的K个物品作为该物品的推荐物品。在线上运行时,当用户浏览了商品p,就可以将商品p对应的相似商品列表直接作为推荐列表返回给前端展示。
这种策略具有可行性的主要原因是,基于ItemCF计算物品相似度矩阵的过程中,物品与物品之间的相似度实际上依赖于用户共同评分的行为。由于单一用户评分过的商品数量实际上是比较少的,并且在短期内(一天),用户新增对商品评分的操作也是比较少的,所以物品相似度矩阵相对来讲是比较稳定的(只会影响当前用户评估过的商品之间的相似度)。
所以相对于UserCF来说ItemCF比较可控和稳定。
ItemCF变种的实际意义就是可以让线上的推荐列表实时的发生变化
矩阵分解
在协同过滤中,我们要求只有当两个用户对于同一个物品进行评分后我们才可以计算用户之间的相似度,或者说只有当两个物品被同一个用户评分后我们才可以计算物品之间的相似度。然而,这样的计算相似度的方式其实是没有考量物品/用户背后的关联性。
举例来说:
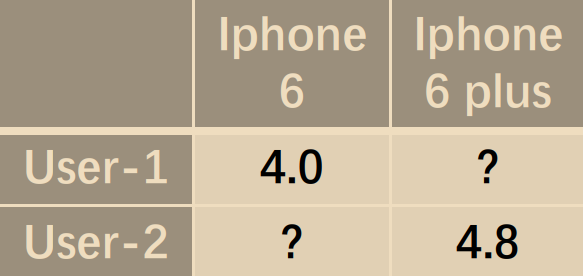
- 用户1对iPhone 6评价为4.0分
- 用户2对iPhone 6 Plus评价为4.8分
问:iPhone 6和iPhone 6 Plus之间的相似度是多少呢?用户1对于iPhone 6 Plus的评分是多少呢?
这里需要指出的是,在传统的协同过滤方法中,iPhone 6和iPhone 6 Plus的相似度将不会直接从用户1和用户2的评分得出。因为传统的协同过滤主要关注同一物品或同一用户的评分,而不太涉及不同物品之间的关联性。
关于用户1对iPhone 6 Plus的评分,根据传统协同过滤方法,无法直接得出。
比如用户对某个商品打了5分、6分或其他具体分数。这引出了一个有趣的问题:为什么用户会给出这样的评分?答案在于,这些商品或服务具有某些特性,这些特性恰恰是用户所需要或所偏好的。换言之,只有当商品呈现出用户所期望的特点时,用户才会给予较高的评分。这意味着商品与用户偏好的契合程度是评分高低的关键因素。相反,如果商品缺乏用户所期待的特点,那么它收到的评分往往会较低。这一过程揭示了用户评分背后的逻辑和推荐系统以此建立更精确推荐的原理。
用户已给iphone6打了4.0分有可能用户希望它有这么几个特点:
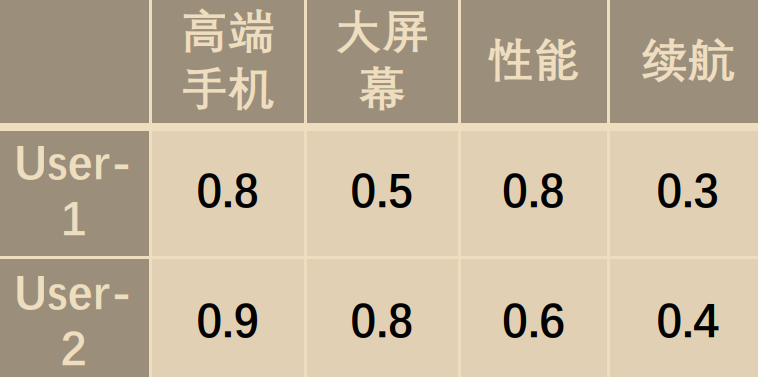
而且IPhone6在这几个特点上具有这么几个信息:
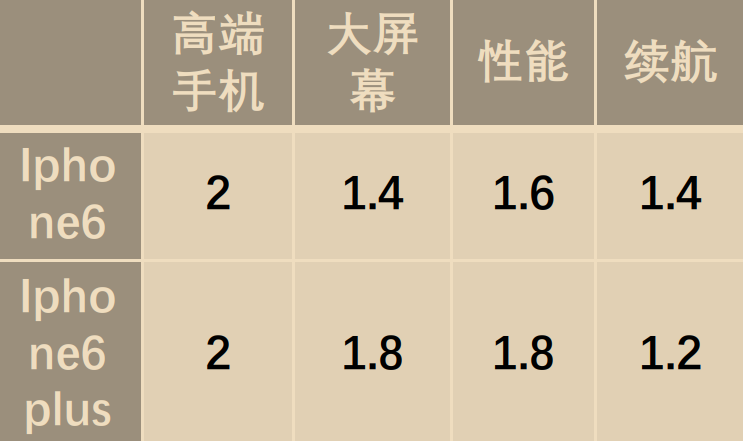
那我们现在把用户一的诉求和iPhone6所具有的特点进行线性组合
我们发现将用户的诉求和IPhone具有的信息线性组合后得到的结果好像正好可以填充问号所在的位置

这其实就是因为我们在构建模型的时候,我们认为用户给这个分值不是无缘无故给的, 而是因为用户考虑了很多方面,那很多方面呢, 就是各方面的因素, 那么我们如何找到这些因素, 我们就看用户对这些因素的偏好到底有多少?以及这个物品包含信息到底有多少?结合起来就是最终的结果。但因素,在模型层面,其实是很难做的。
隐语义模型
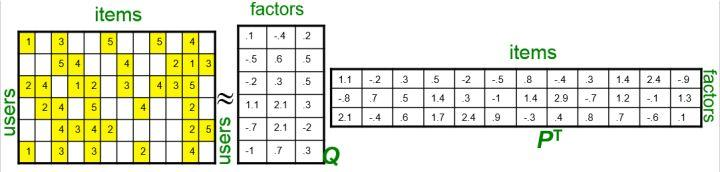
隐语义模型又叫做潜在因子算法(Latent Factor)。其算法思想是:认为每个用户都有自己的偏好,同时每个物品也包含所有用户的偏好信息。因此,可以认为用户对于物品的高评分体现的是物品中所包含的偏好信息恰好就是用户喜好的信息。然而,这个偏好信息却无法简单且明显地找出,因此我们可以认为这个偏好信息就是潜在影响用户对物品评分的因子,即潜在因子。因此,只要我们可以得到用户-潜在因子矩阵Q和物品-潜在因子矩阵P,就可以计算出用户对于物品的评分信息。 \[ \hat{R}=QP^T \] 比如说我们做一个电影推荐,我们能知道影响用户对电影评分的因素到底有哪些吗?这些因素是不可感知的,所以, 我们给它取了个名字叫做隐因子,或者说潜在因子。所以它叫做隐语义模型,又叫作潜在因子算法,而这个算法的本质思想就是认为每个用户都有自己的偏好,每个物品也有自己的偏好信息。只有当用户的偏好信息和物品的偏好信息刚好契合的时候,用户才会给出一个高的评分。也就是说用户对物品的高评分其实体现的是物品包含的某些信息恰好是用户所喜好的,于是用户就给了高评分,但是这个偏好信息, 实际上我们是没法很明显地直接找出来的, 但我们不管,因为实际上我们可以认为用户对物品的评分等于用户潜在因子矩阵Q乘上物品潜在因子矩阵P。
用户-潜在因子矩阵Q:1表示特别喜欢,0表示不喜欢。 \[ \begin{array}{|l|r|r|r|r|r|} \hline & \text { 小清新 } & \text { 重口味 } & \text { 优雅 } & \text { 伤感 } & \text { 五月天 } \\ \hline \text { 张三 } & 0.6 & 0.8 & 0.1 & 0.1 & 0.7 \\ \hline \text { 李四 } & 0.1 & 0 & 0.9 & 0.1 & 0.2 \\ \hline \text { 王五 } & 0.5 & 0.7 & 0.9 & 0.9 & 0 \\ \hline \end{array} \] 物品-潜在因子矩阵P:表示各个物品包含各个元素的成分,比如音乐A是一个偏小清新的音乐, 包含小清新这个Latent Factor的成分是0.9,重口味的成分是0.1,优雅的成分是0.2....
| 小清新 | 重口味 | 优雅 | 伤感 | 五月天 | |
|---|---|---|---|---|---|
| 音乐A | 0.9 | 0.1 | 0.2 | 0.4 | 0 |
| 音乐B | 0.5 | 0.6 | 0.1 | 0.9 | 1 |
| 音乐C | 0.1 | 0.2 | 0.5 | 0.1 | 0 |
| 音乐D | 0 | 0.6 | 0.1 | 0.2 | 0 |
| 小清新 | 重口味 | 优雅 | 伤感 | 五月天 | 音乐A | 音乐B | 音乐C | 音乐D | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 张三 | 0.6 | 0.8 | 0.1 | 0.1 | 0.7 | 张三 | 0.68 | 1.58 | 0.28 | 0.51 | |
| 李四 | 0.1 | 0 | 0.9 | 0.1 | 0.2 | 李四 | 0.31 | 0.43 | 0.47 | 0.11 | |
| 王五 | 0.5 | 0.7 | 0.9 | 0.9 | 0 | 王五 | 1.06 | 1.57 | 0.73 | 0.69 |
根据矩阵Q和P,就可以计算出每个人对每个商品的喜好程度。比如,张三对音乐A的喜好程度可以表示为:张三对小清新的偏好*以音乐A含有的小清新的成分+张三对重口味的偏好乘以音乐A含有的重口味的成分再加上张三对优雅的偏好乘以音乐A含有的优雅的成分等等。即:\(0.6*0.9 + 0.8*0.1 + 0.1*0.2 + 0.1*0.4 + 0.7*0 = 0.68\)
| 小清新 | 重口味 | 优雅 | 伤感 | 五月天 | 小清新 | 重口味 | 优雅 | 伤感 | 五月天 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 张三 | 0.6 | 0.8 | 0.1 | 0.1 | 0.7 | 音乐A | 0.9 | 0.1 | 0.2 | 0.4 | 0 |
根据Q和P通过这种计算方式就可以得到不同用户对于不同物品的评分矩阵,最终的推荐结果就是每个人评分比较高的那些物品,比如张三就推荐音乐B,李四推荐音乐C,王五推荐音乐B。
| 音乐A | 音乐B | 音乐C | 音乐D | |
|---|---|---|---|---|
| 张三 | 0.68 | 1.58 | 0.28 | 0.51 |
| 李四 | 0.31 | 0.43 | 0.47 | 0.11 |
| 王五 | 1.06 | 1.57 | 0.73 | 0.69 |
不过以上数据都是我们人为填的:
求解用户/物品-潜在因子矩阵的过程如下:
- 假定有\(n\)个用户,\(m\)个物品,\(k/K\)个隐因子;
- \(R\)为用户-物品评分矩阵,\(Q\)为用户-潜在因子矩阵,\(P\)为物品-潜在因子矩阵。
\[ 在用户-潜在因子矩阵和物品-潜在因子矩阵未求出前R_{n*m}是个稀疏矩阵\\ R_{n^*m}\approx Q_{n^*k}\times P_{m^*k}^T\quad\hat{r}_{ui}=q_up_i^T=\sum_{k=1}^Kq_{uk}p_{ik}\\ \ \ \ \ \ \quad \quad \quad当Q_{n^*k}和P_{m^*k}^T求出来后, R_{n*m}就是一个稠密的矩阵, 相当于我们已经做预测了 \]
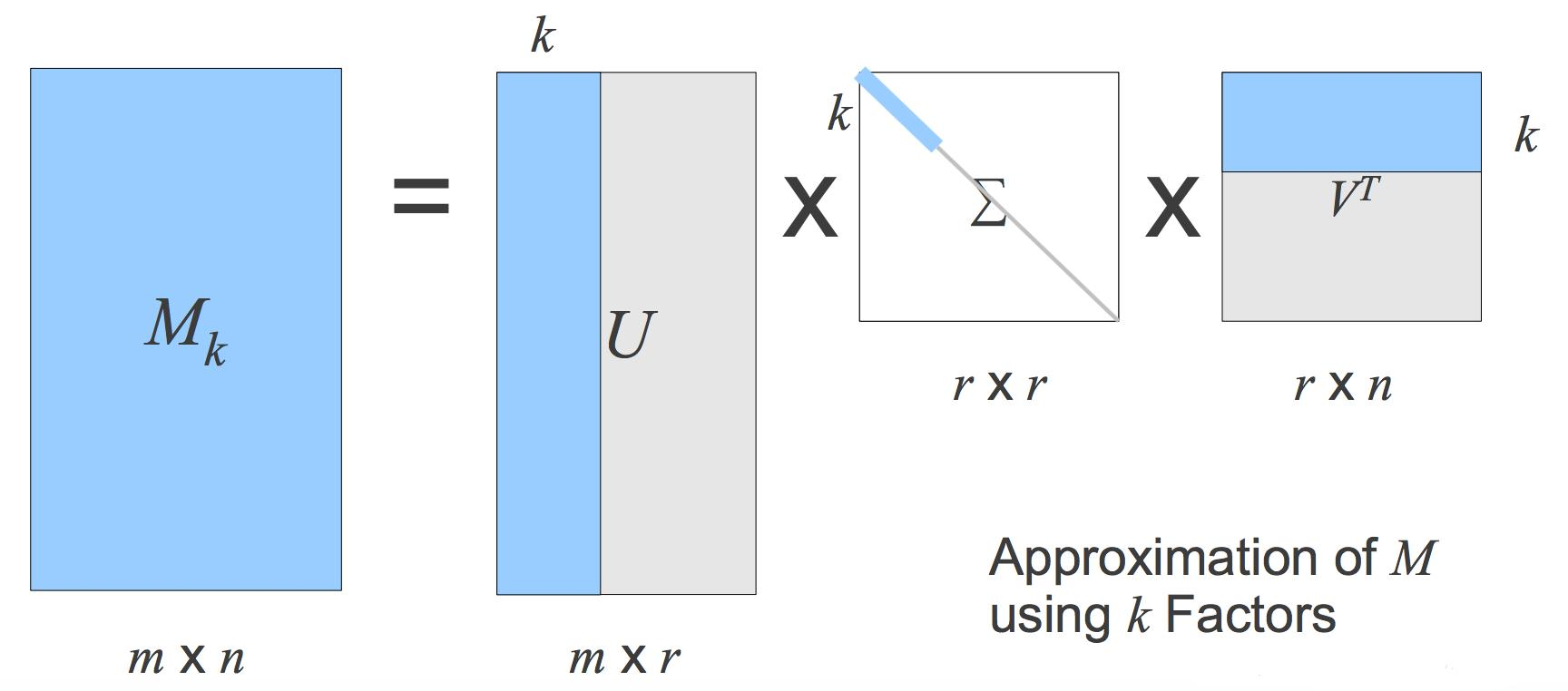
SVD
SVD(奇异值分解,Singular Value Decomposition)的想法是根据已有的评分情况,分析出评分者对各个物品因子的喜好程度,以及各个物品对于这些因子的包含程度,最后再根据分析结果预测评分。通过SVD的方式可以找出影响评分的显式因子和隐藏因子,从而发现更多有意义的关联关系。
SVD的数学定义:将给定评分矩阵\(R\)分解成为三个矩阵的乘积,其中\(U\)、\(V\)称为左、右奇异向量,\(\Sigma\)对角线上的值称为奇异值;其中\(R\)为\(n \times
m\)的矩阵,\(U\)为\(n \times n\)的矩阵,\(\Sigma\)为\(n
\times m\)的矩阵,\(V\)为\(m \times m\)的矩阵。可以使用前\(k\)个奇异值来近似地替代\(R\)矩阵,因为前1%的奇异值的和就占了全部奇异值和的99%以上。
\[
R_{n^*m}=U_{n^*n}*\sum_{n^*m}*V_{m^*m}\quad R_{n^*m}\approx
U_{n^*k}*\sum_{k^*k}*V_{k^*m}^T
\] 
数学层面的SVD分解要求用户-物品评分矩阵必须是稠密的,也就是说用户-物品评分矩阵的所有位置不能有空白, 有空白时我们是没法直接进行SVD分解的。但是如果这个矩阵是稠密的,那不就是说我们已经找到所有用户物品的评分了吗?那我们还进行SVD做什么?所以数学层面的SVD不能做。这是一个问题,传统SVD采用的方法是对评分矩阵中的缺失值进行简单的补全,比如用全局平均值或者用用户物品平均值补全,得到补全后的矩阵。接着可以用SVD分解。
使用上述简单的矩阵分解方式虽然可以解决缺失值的情况,但由于推荐系统中的用户量和物品量特别大,直接使用原始SVD的矩阵分解是比较困难的。
FunkSVD
由于现在在SVD矩阵分解中,将矩阵分解为三个矩阵效率比较低,那么我们可以通过矩阵分解为两个矩阵来降低执行的消耗;即将\(U\)、\(V\)矩阵进行转换得到用户因子矩阵\(Q\)和物品因子矩阵\(P\),并且最终的评分预测为\(r_{ui}\)也需要进行对应的转换。
对角线矩阵\(\Sigma\)中, 因为靠前的奇异值占总奇异值的比例非常高, 所以我们只取前面一部分, 也就是我们对\(\Sigma\)进行截取, 而当我们对\(\Sigma\)进行截取后, 我们也要对\(U和V\)矩阵进行截取才能满足矩阵运算。并且截取过后我们会发现对角线矩阵中的奇异值都是大于零的值, 所以我们是可以将对角线矩阵\(\Sigma\)分成两个\(\sqrt{\Sigma}\)相乘的形式, 然后分别与\(U和V\)矩阵组合为一个整体。 \[ \begin{aligned} & Q_{n^* k}=U_{n^* k} *\left(\Sigma_{k^* k}\right)^{1 / 2} \quad P_{m^* k}=\left(\left(\Sigma_{k^* k}\right)^{1 / 2} \times V_{m^* k}^T\right)^T \\ & R_{\mathrm{n}^* m} \approx Q_{n^* k} * P_{m^* k}^T \\ & \hat{r}_{u i}=q_u p_i^T=\sum_{k=1}^K q_{u k} p_{i k} \end{aligned} \] 实际上, 我们直接做矩阵分解不行, 但是我们可以做一件事, 用算法的思路去做, 因为原始的用户-物品评分矩阵是稀疏的, 也就是说存在很多空白位置, 并且这个空白位置的值我们也不知道是什么, 但是我们只要把黄色区域的值给预测正确不就行了, 而空白位置我们可以认为预测的结果没有问题。
详细来说,用户因子矩阵\(Q\)和物品因子矩阵\(P\)的计算可以利用线性回归的思想,通过随机梯度下降的方式进行学习,迭代式地更新相关参数即可。使用SVD矩阵因子分解推荐算法对于评分稀疏矩阵也可以进行正常处理,对于没有评分的部分不用计算误差值,直接令误差值为0。
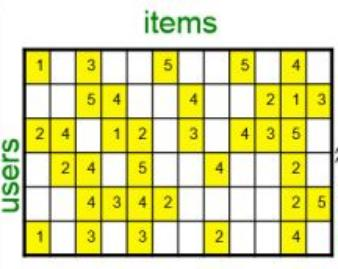 \[
\begin{aligned}
& \hat{r}_{u i}=q_u p_i^T \quad e_{u i}=r_{u i}-\hat{r}_{u i} \\
& \min _{p, q} \frac{1}{2} \sum_{u, i}\left(r_{u, i}-q_u
p_i^T\right)^2 \\
& p_i^{k+1}=p_i^k+\alpha \cdot e_{u i} \cdot q_u^k \\
& q_u^{k+1}=q_u^k+\alpha \cdot e_{u i} \cdot p_i^k
\end{aligned}
\] 这其实就是一个回归模型,
只不过是按照矩阵分解的思路构建出来的。并且我们现在不用做矩阵分解了,我们还是用算法的思路去做,我们去构建预测值和实际值,然后计算误差,然后我们合并在一起,然后梯度下降求参,这样就可以了。
\[
\begin{aligned}
& \hat{r}_{u i}=q_u p_i^T \quad e_{u i}=r_{u i}-\hat{r}_{u i} \\
& \min _{p, q} \frac{1}{2} \sum_{u, i}\left(r_{u, i}-q_u
p_i^T\right)^2 \\
& p_i^{k+1}=p_i^k+\alpha \cdot e_{u i} \cdot q_u^k \\
& q_u^{k+1}=q_u^k+\alpha \cdot e_{u i} \cdot p_i^k
\end{aligned}
\] 这其实就是一个回归模型,
只不过是按照矩阵分解的思路构建出来的。并且我们现在不用做矩阵分解了,我们还是用算法的思路去做,我们去构建预测值和实际值,然后计算误差,然后我们合并在一起,然后梯度下降求参,这样就可以了。
在普通的SVD求解过程中,和机器学习类似,我们也需要防止\(Q\)和\(P\)的隐因子值不能过大,所以我们加入正则化项;从而可以得到下列目标函数: \[ \begin{gathered} \hat{r}_{u i}=q_u p_i^T \quad e_{u i}=r_{u i}-\hat{r}_{u i} \\ \min _{q_s, p_*} \frac{1}{2}\left(\sum_{u, i}\left(r_{u, i}-q_u p_i^T\right)^2+\lambda\left(\left\|q_u\right\|^2+\left\|p_i\right\|^2\right)\right) \\ p_i^{k+1}=p_i^k+\alpha \cdot\left(e_{u i} \cdot q_u^k-\lambda \cdot p_i^k\right) \\ q_u^{k+1}=q_u^k+\alpha \cdot\left(e_{u i} \cdot p_i^k-\lambda \cdot q_u^k\right) \end{gathered} \]
BiasSVD
同普通的协同过滤算法一样,我们可以更改一下FunkSVD预测值公式,可以认为最终的预测值是在基准评分/偏置项基础上的一个变化,从而我们可以得到下列预测公式:
同样的我们可以得到一个加入正则化项后的目标函数:
\[
\begin{gathered}
\hat{r}_{u i}=\mu+b_u+b_i+q_u p_i^T \\
e_{u i}=r_{u i}-\hat{r}_{u i} \\
\min _{q_u, p_i, b_u, b_i} \frac{1}{2}\left(\sum_{u, i}\left(r_{u,
i}-\hat{r}_{u,
i}\right)^2+\lambda\left(b_u^2+b_i^2+\left\|q_u\right\|^2+\left\|p_i\right\|^2\right)\right)
\end{gathered}
\] 通过梯度下降法,我们最终可以得到b、q、p的迭代计算公式: \[
\begin{gathered}
e_{u i}=r_{u i}-\hat{r}_{u i}\ \ \ \ \ \min _{q_u, p_i, b_u, b_i}
\frac{1}{2}\left(\sum_{u, i}\left(r_{u, i}-\hat{r}_{u,
i}\right)^2+\lambda\left(b_u^2+b_i^2+\left\|q_u\right\|^2+\left\|p_i\right\|^2\right)\right)
\\
b_u^{k+1}=b_u^k+\alpha \cdot\left(e_{u i}-\lambda \cdot b_u^k\right) \\
b_i^{k+1}=b_i^k+\alpha \cdot\left(e_{u i}-\lambda \cdot b_i^k\right) \\
p_i^{k+1}=p_i^k+\alpha \cdot\left(e_{u i} \cdot q_u^k-\lambda \cdot
p_i^k\right) \\
q_u^{k+1}=q_u^k+\alpha \cdot\left(e_{u i} \cdot p_i^k-\lambda \cdot
q_u^k\right)
\end{gathered}
\]
SVD++
SVD++算法是在BiasSVD算法的基础上加入了用户的隐式反馈;在BiasSVD矩阵 分解中其实是没有考虑过用户隐式的反馈信息,比如浏览行为、点击行为等;所以可以在目标函数中加入这些隐式数据作为新的参数,从而得到一个新的预测公式为:
对于该公式同样可以使用梯度下降法分别求解出\(bu\)、\(bi\)、\(qu\)、\(yj\)、\(pi\)的值。 \[ \hat{r}_{ui}=\mu+b_u+b_i+\Bigg(q_u+\Bigg|I_u\Bigg|^{-\frac12}\sum_{j\in I_u}y_j\Bigg)p_i^T \]
- \(y_j\)是与用户u互动过的物品 j 的潜在因子向量(也可称为隐式反馈向量)。
- \(\Bigg|I_u\Bigg|\) 是该集合中物品的数量
这样就相当于用户对于各个因子的这样一个偏好,不仅仅由用户本身的向量\(q_u\)表示,同时还和用户已经评论过的商品有关, 因为这些商品可能会有一些隐式的反馈。
SVD++的效果确实很好, 不过它很大的一个问题就是速度很慢, 几乎不能用。
推荐算法_关联规则
关联规则挖掘是一种在大规模交易中识别类似规则关系模式的通用技术,也是可以应用到推荐系统中的一种传统算法。
交易 $ T $ 是所有有效产品集合 $ P = {p_1, p_2, , p_n} $ 的子集,表示被一起购买的产品集合,关联规则 $ X Y $ 表示只要交易 $ T $ 中包含了 $ X $ 里面的元素,那么认为 $ Y $ 里面的元素也有可能被 $ T $ 包含。常见的规则挖掘算法是Apriori算法,关联规则的衡量指标是:支持度(support)和可信度(confidence)。
在关联规则挖掘中,交易集(Transaction Set)是由多个交易(Transaction)组成的集合。每个交易是一个项集(Item Set),包含若干项(Item)。关联规则挖掘的目标是发现项集之间的有趣关系或模式。
在推荐系统的关联规则算法中,“交易”这个名词可以有多种含义,具体取决于应用场景和数据的类型。最常用的几种含义包括用户行为交易、购物车交易、会话交易、评分交易和购买历史交易。这些交易数据用于挖掘用户行为模式,从而为用户提供个性化的推荐。所以“交易”一词我们可以打个引号。
例如: \[ \begin{array}{|ll|} \hline \text { 交易ID } & \text { 商品项集 } \\ \hline 1 & \text { 牛奶, 面包, 黄油 } \\ \hline 2 & \text { 啤酒, 面包 } \\ \hline3 & \text { 牛奶, 面包, 啤酒, 黄油 } \\ \hline 4 & \text { 面包, 黄油 } \\ \hline 5 & \text { 牛奶, 黄油 } \\ \hline \end{array} \] 在这个例子中,每一行代表一个交易,每个交易包含一个项集,项集中的每个项代表一个商品。
Apriori
Apriori算法是常用的用于挖掘出数据关联规则的算法。它用来找出数据值中频繁出现的数据集合,这些找出的集合有助于我们的业务决策。同时,我们也可以认为这些频繁出现的数据集合中的数据项存在一定的关联性。简而言之,可以认为这些数据项之间存在某种“相似性”。
举例来说,在电商的网购数据中,如果发现某些商品经常一起被购买,那么我们可以认为这些商品之间存在某种“相似性”。因此,我们可以优化网站中这些商品的排列位置、优化商品的仓库位置或者将这些“相似”的物品推荐给正在浏览对应物品的客户。这样做可以达到增加经济效益、节约成本的目的。
基本概念:
交易集:包含所有数据的一个数据集合,数据集合中的每条数据都是一笔交易。
项:交易集中的每个商品被称为一个项。
模式/项集(ItemSet):项组合被称为模式/项集。
支持度(Support):一个项集在整个交易集中出现的次数或频度。例如,Support({A, C})=2 表示 A 和 C 同时出现的次数是 2 次。
最小支持度:当交易次数支持度达到最小支持度的情况下,该项集才会被计算。
频繁项集:如果项集的支持度大于等于最小支持度,那么该项集被称为频繁项集。
置信度(Confidence):关联规则左件和右件同时出现的频繁程度。该值越大,表示同时出现的几率越大。
关联规则:$ () $ 表示如果客户购买了左件(LHS),也可能购买右件(RHS),购买的置信度为 confidence。
比如:在购物数据中, 啤酒对应尿布的置信度为 \(70 \%\), 支持度为 \(30 \%\) 。则意味着在所有购物数据中, 总共有 \(30 \%\) 的用户既买啤酒又买尿布; 同时在买啤酒的用户中有 \(70 \%\) 的用户购买尿布。 \[ \begin{gathered} \text { Support }_{\text {rule }}(X, Y)=\frac{X \cap Y \text { 的数据量 }}{\text { 总的数据量 }} \\ \text { Confidence }_{\text {rule }}(X, Y)=\frac{X \cap Y \text { 的数据量 }}{\text { 含 } X \text { 的数据量 }} \end{gathered} \] Apriori算法的本质作用是找出购物数据集中的最频繁的K项集。该算法采用了迭代的方法。首先搜索出候选1项集及对应的支持度,然后剪枝去掉低于最小支持度的1项集,得到频繁1项集。接着对剩下的频繁1项集进行连接,得到候选的频繁2项集,筛选去掉低于最小支持度的候选频繁2项集,得到频繁2项集,以此类推,迭代下去,直到无法找到频繁k+1项集为止。对应的频繁k项集的集合即为算法的输出结果。

输入:数据集合D, 支持度阈值 \(\alpha\) ;输出:最大的频繁K项集
- 扫描整个数据集,得到所有出现过的1项集,得到候选频繁1项集。
- 令 \(\mathrm{k}=1\)
- 挖掘频繁 \(k\) 项集
- 扫描数据计算候选频繁 \(k\) 项集的支持度
- 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k 项集为空, 则直接返回频繁 \(k-1\) 项集的集合作为算法结果,算法结束。如果得到的频繁 \(k\)项集只有一项, 则直接返回频繁 \(k\) 项集的集合作为算法结果, 算法结束。
- 基于频繁k项集和频繁1项集,连接生成候选频繁k+1项集。
- \(k=k+1\), 转入步骤 3 。
FP Tree
Apriori算法作为挖掘频繁项集的算法,需要多次扫描数据,因此存在I/O瓶颈比较高的问题。为了解决这个问题,提出了FP-Tree算法,也称为FP Growth算法。在FP-Tree算法中,不管存在多少数据量、不管频繁K项集的K有多大,只需要扫描两次数据集,因此提高了算法的运行效率。
FP-Tree算法改进了Apriori算法的I/O瓶颈,利用树结构来提高算法的执行效率,是一种利用空间换时间的一种算法效率提升方式。
备注:FP-Tree是我们在生产环境中常用的一种数据挖掘频繁项集的算法。
为了减少I/O次数,FP-Tree算法引入了一些数据结构来临时存储数据,主要包含三个部分:
- 项头表:记录所有的1项频繁集以及出现的次数,按照次数降序排列。
- FP-Tree:将原始数据集映射到内存中的一棵FP树。
- 节点链表:是在项头表中存储的一个链表,链表中存储的是具体在FP-Tree中存储的对应节点位置。
FP-Tree算法可以分为以下两个过程:
- 项头表和FP-Tree的构建(同时构建节点链表)。
- FP-Tree的挖掘。
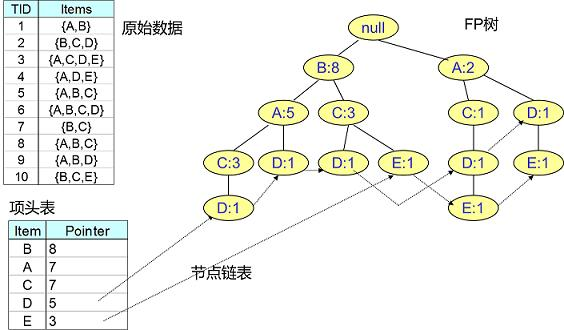
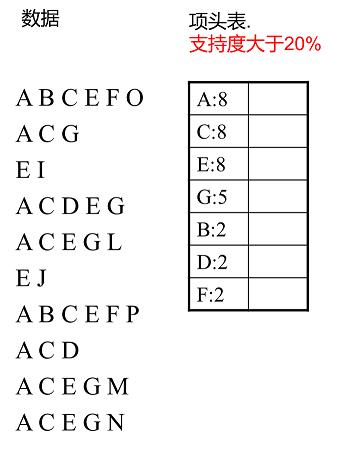
扫描所有数据,得到所有一项集的支持度,然后删除支持度低于阈值的项,得到频繁一项集,将所有频繁一项集按照支持度降序排列,放入项头表中。
FP-Tree树的构建是FP-Tree算法的关键点,主要分为两个过程:
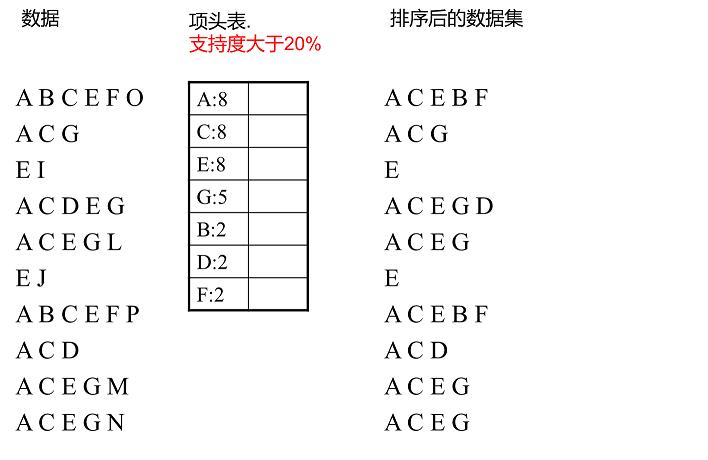
扫描数据,对于每条数据删除非频繁的1项集,并按照支持度降序排列(按照项头表),得到排序后的数据集。
将排序好的数据直接插入到建FP-Tree。初始状态FP树是空的,建立FP树时我们一条条地读入排序后的数据集,插入FP树。插入时按照排序后的顺序,插入FP树中,排序靠前的节点是祖先节点,而靠后的是子孙节点。如果有共用的祖先,则对应的公用祖先节点计数加1。插入后,如果有新节点出现,则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后,FP树的建立完成。
获取排序数据:
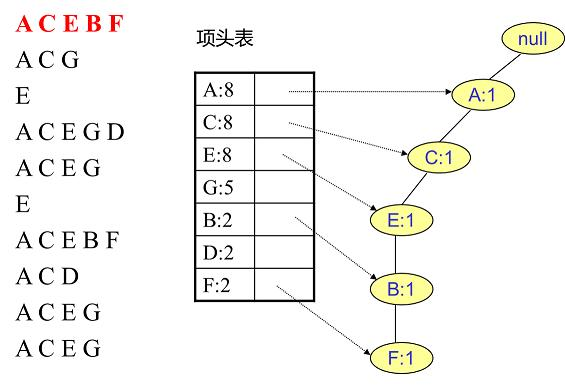
插入第一条数据:
插入第二条数据:

插入第三条数据:
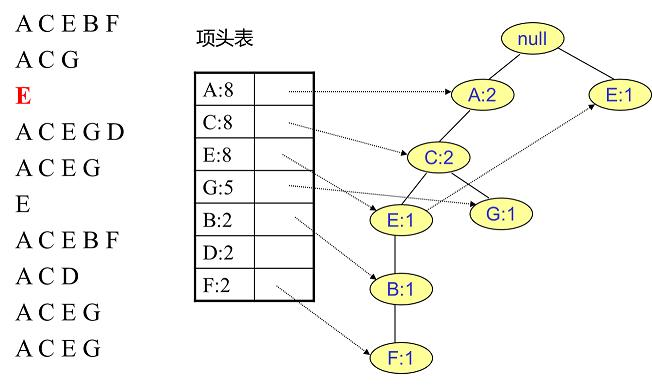
插入第四条数据:
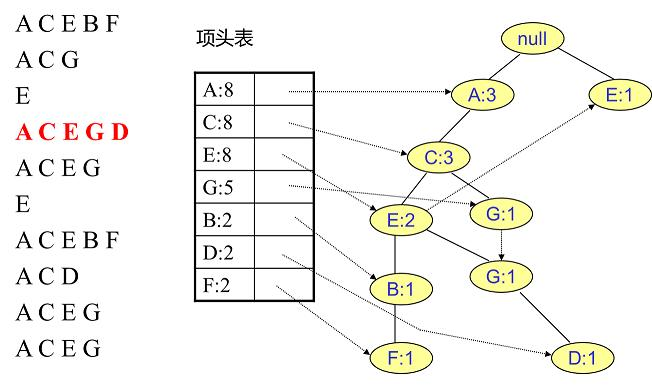
插入第五条数据:
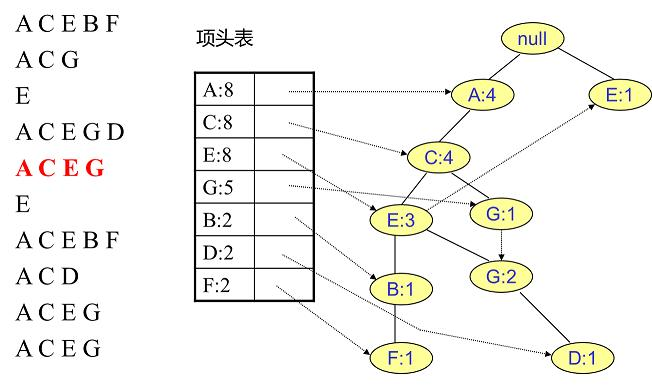
插入第六条数据:
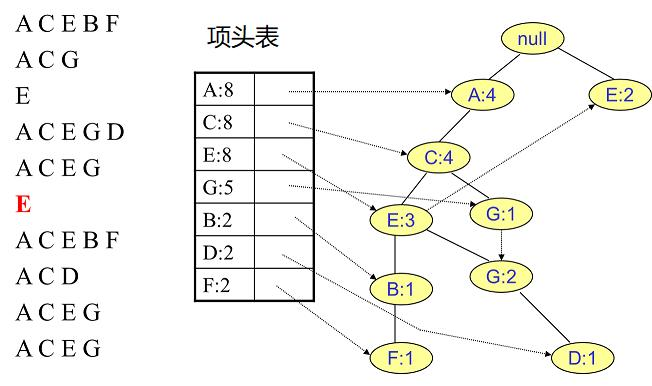
插入第七条数据:
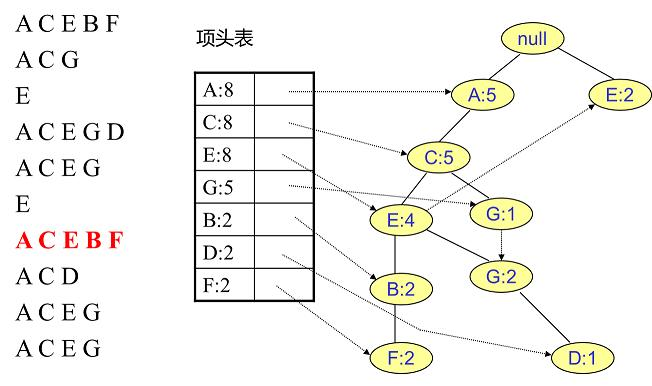
插入第八条数据:

插入第九条数据:
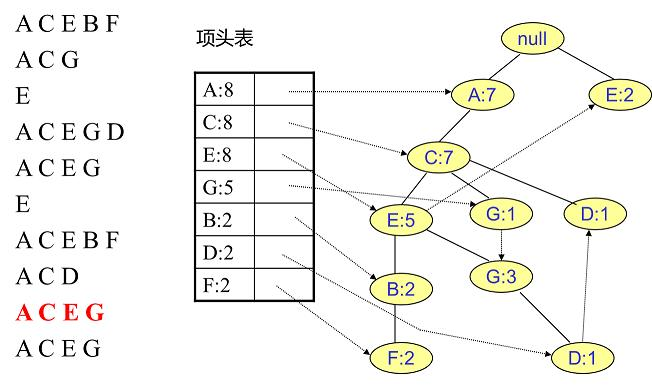
插入第十条数据:
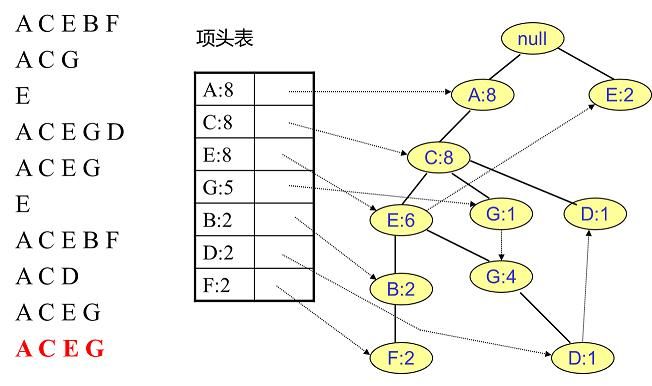
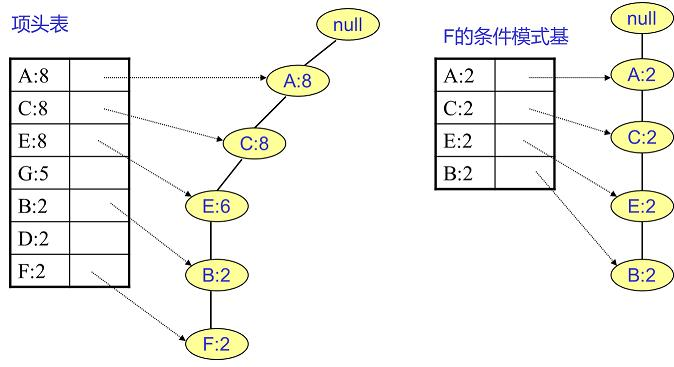
这颗FP树就表达了当前数据中所有商品的组合形式。当构建好FP树、项头表以及节点链表后,就可以开始进行频繁项集的挖掘了。首先从项头表的底部项依次向上挖掘,对于项头表对应于FP树的每一项,找出对应的条件模式基,所谓条件模式基是以我们要挖掘的节点作为叶子节点所对应的FP子树,得到这个FP子树,我们将子树中每个非叶子节点的的计数设置为其所有叶子节点的计数和,然后求每个项的总的计数和,并且删除计数低于支持度的节点。从这个条件模式基,我们就可以递归挖掘得到频繁项集了。
寻找F节点的条件模式基:
我们很容易得到F的频繁2项集为{A:2, F:2}、{C:2, F:2}、{E:2, F:2}、{B:2, F:2}。递归合并二项集,得到频繁三项集为{A:2, C:2, F:2}、{A:2, E:2, F:2},...。当然一直递归下去,最大的频繁项集为频繁5项集,为{A:2, C:2, E:2, B:2, F:2}。
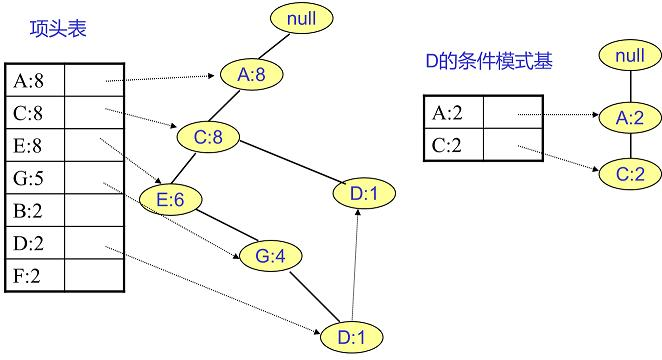
寻找D节点的条件模式基 D的频繁2项集为{A:2,D:2}、{C:2,D:2}。递归合并二项集,得到频繁三项集为{A:2,C:2,D:2}。D 对应的最大的频繁项集为频繁3项集
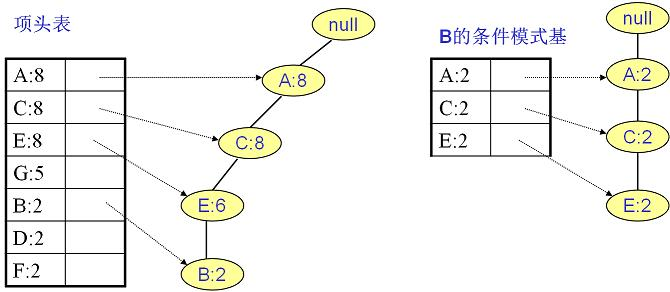
寻找B节点的条件模式基 B的频繁2项集为{A:2,B:2}、{C:2,B:2}、{E:2,B:2}。递归合并二项集,得到频繁三项集为 {A:2,C:2,B:2}、{A:2,E:2,B:2}、{E:2,C:2,B:2}。递归挖掘到B的最大频繁项集为频繁4项集{A:2, C:2, E:2,B:2}。
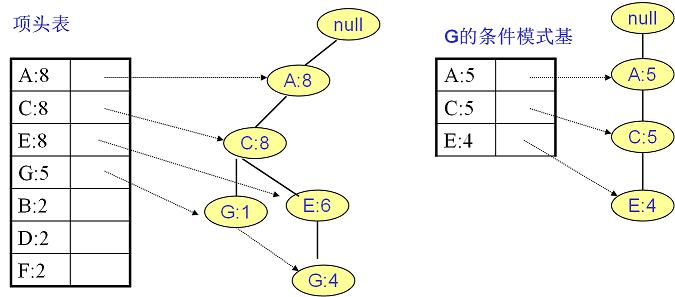
寻找G节点的条件模式基 G的频繁2项集为{A:5,G:5}、{C:5,G:5}、{E:4,G:4}。递归合并二项集,得到频繁三项集为 {A:5,C:5,G:5}、{A:4,E:4,G:4}、{E:4,C:4,G:4}。递归挖掘到G的最大频繁项集为频繁4项集{A:4, C:4, E:4, G:4}。
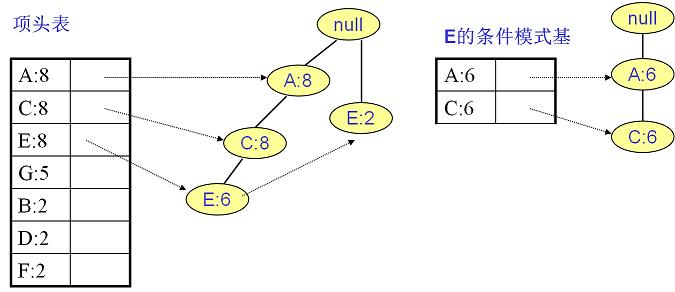
寻找E节点的条件模式基 E的频繁2项集为{A:6,E:6}、{C:6,E:6}。递归合并二项集。递归挖掘到E的最大频繁项集为频繁 3项集{A:6, C:6, E:6}。
寻找C节点的条件模式基 C的频繁2项集为{A:8,C:8},即C的最大频繁项集为频繁2项集{A:8,C:8}。
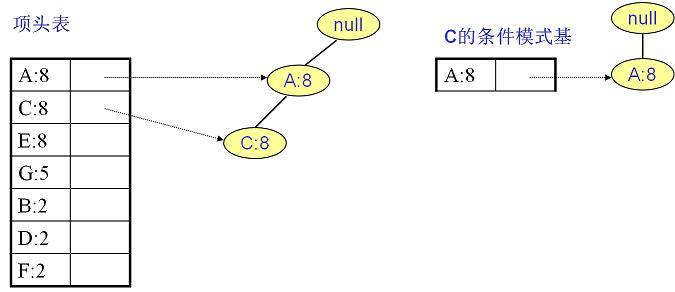
条件模式基是以所查找节点为结尾的路径集合。简而言之,一条前缀路径就是介于所查找节点与根节点之间的所有元素。 例如:I3在FP树中一共出现了3次,其祖先路径分别是{I2,I1:2},{I2:2}和{I1:2}。这3个祖先路径的集合就是频繁项I3的条件模式基。
频繁2项集: \(\{A:8, C:8\}, \{A:6, E:6\}, \{C:6, E:6\}, \{A:5, G:5\}, \{C:5, G:5\}, \{E:4, G:4\}, \{A:2, B:2\},\{C:2, B:2\}, \{E:2, B:2\}, \{A:2, D:2\}, \\ \{C:2, D:2\}, \{A:2, F:2\}, \{C:2, F:2\}, \{E:2, F:2\}, \{B:2, F:2\}\)
频繁3项集: \(\{A:6, C:6, E:6\}, \{A:5, C:5, G:5\}, \{A:4, E:4, G:4\}, \{E:4, C:4, G:4\}, \{A:2, C:2, B:2\}, \{A:2, E:2, B:2\}, \{E:2, C:2, B:2\}, \\\{A:2, C:2, D:2\}, \{A:2, C:2, F:2\}, \{A:2, E:2,F : 2\}, \{A : 2,B : 2,F : 2\}, \{C : 2,E : 2,F : 2\}, \{C : 2,B : 2,F : 2\}, \{E : 2,B : 2,F : 2\}\)
频繁4项集: \(\{A : 2,C : 2,E : 2,F : 2\}, \{A : 2,C : 2,B : 2,F : 2\}, \{C : 2,E : 3,B : F : G \}\)
频繁5项集: \(\{A : 1,C : E : B : F \}\)
FP-Tree算法流程主要包括以下几步:
扫描数据,得到所有的频繁1项集的计数,然后删除支持度低于阈值的项,将1项频繁集放入项头表,并按照支持度降序排列。
读取数据集中的每条数据,将每条数据中的非频繁1项集(项)删除,并按照项头表中的项顺序对项进行排列,然后将排列后的数据插入到FP树中,插入时按照排序后的顺序插入,并计算当前节点的后序子孙节点的数目。直到所有数据均插入到FP树后,FP树构建完成。
从项头表的底部项依次向上找到项头表项对应的条件模式基。从条件模式基递归挖掘得到项头表项的频繁项集。
如果不限制频繁项集的项数,则返回上一步骤的所有的频繁项集,否则只返回满足项数要求的频繁项集。
用机器学习算法做推荐
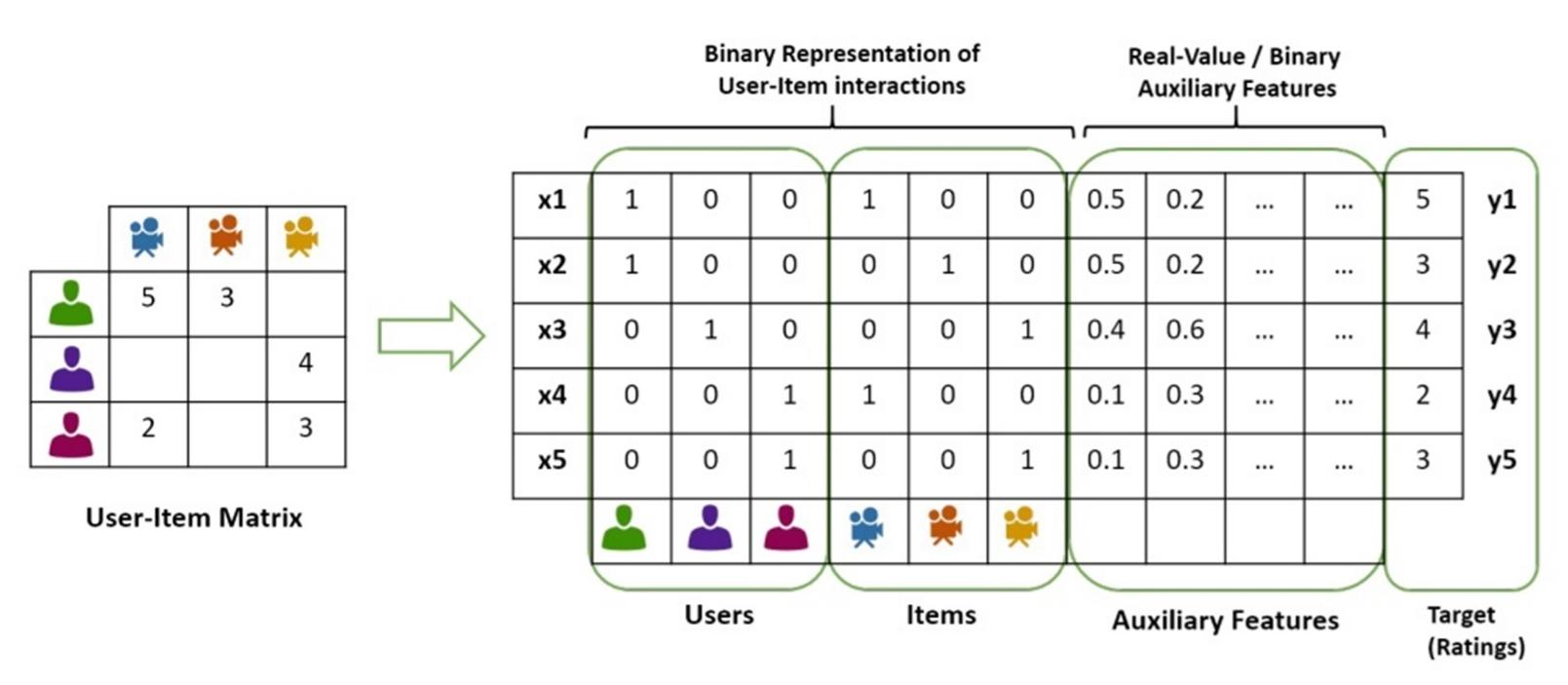
因为机器学习算法输入的数据是特征属性矩阵, 而我们在之前的推荐算法(协同过滤、矩阵分解、关联规则等)中使用的输入数据都是用户-物品评分矩阵, 所以我们需要将用户-物品评分矩阵转化为特征属性矩阵。但是特征属性矩阵嘛, 除了对用户id和物品id做独热编码之外, 实际上来讲我们也会做一些其他的特征信息, 类似于一些交叉的特征信息。
推荐算法—LR
LR:逻辑回归算法,是机器学习领域中常用的线性分类算法;将LR算法应用到推荐领域是一种非常经典常用的使用方式,一般用于预测用户对于商品是否点击、是否购买、是否观看、是否添加购物车等操作,也就是常用的CTR(Click through rate;点击率)预估和CVR(Conversion Rate;转化率)预估,也就是将推荐转换为 二分类问题来建模。 \[ \begin{aligned} & p=\operatorname{sigmoid}(w x+b) \\ & \text { loss }=-\sum(y * \ln p+(1-y) * \ln (1-p)) \\ & w^{’}=w-\alpha * \frac{\partial l o s s}{\partial w} \\ & b^{’}=b-\alpha * \frac{\partial \operatorname{loss}}{\partial b} \end{aligned} \]
推荐算法—GBDT+LR
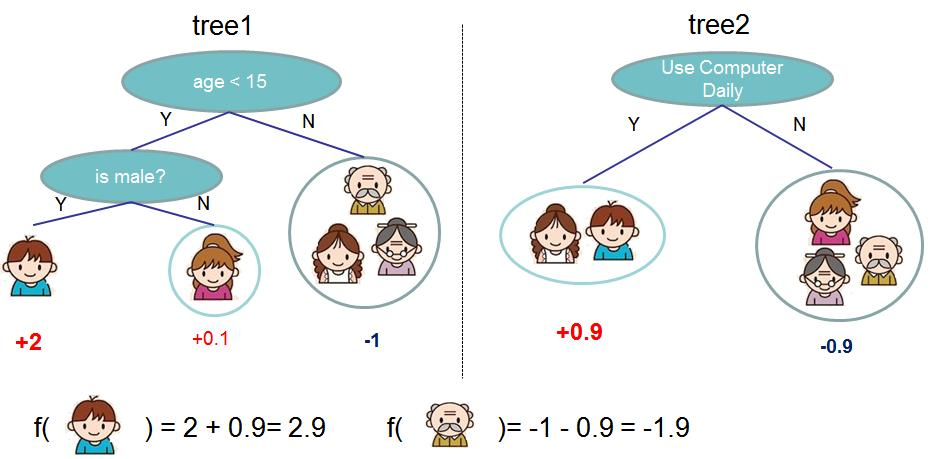
GBDT是一种基于决策树思路的集成算法,由于决策树本身的特性具有特征选择的功能,但是在 推荐领域中经过OneHot编码之后的特征是一种高维稀疏的特征矩阵,直接使用LR模型效果比较 差,所以在传统的推荐领域中,建议采用GBDT这种基于树结构的集成算法来进行LR模型前的特 征组合或者特征转换/映射,而且采用GBDT+LR的结构具有解释性强的特点,在某些特定领域中, 该策略还是一种非常强的推荐策略。
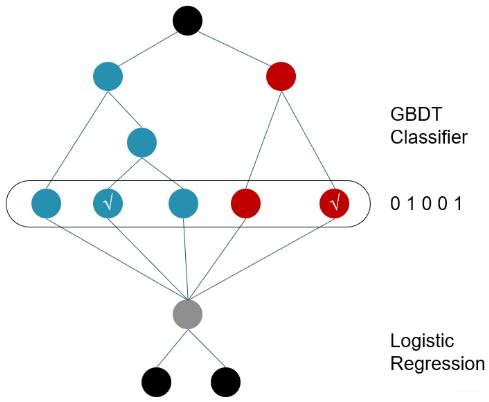
sklearn中的GBDT分类器底层实际上是回归决策树, 且在每个子模型中每个类别都对应一个回归决策树
推荐算法—FM(Factorization Machines)
由于 \(LR\) 模型假设特征之间是相互独立的, 忽略了特征之间关系等高阶信息;在 \(L R\) 中, 特征组合等高阶信息是通过特征工程在特征侧引入的,比如多项式扩展+LR、GBDT+LR等方式;
逻辑回归模型根据现有的特征构建一个线性决策边界,将数据分类。在逻辑回归中,每个特征对结果的贡献是加权和的形式,也就是说,每个特征都有一个相关的权重。逻辑回归模型虽然能够捕捉特征之间的线性关系,但在处理每个特征对输出概率影响的时候,它并不直接考虑特征之间的相互作用。逻辑回归考虑的是特征与输出之间的线性关系,而没有直接考虑特征之间相互作用的高阶信息。让我们通过比较逻辑回归和决策树模型来说明这一点。
逻辑回归 (LR)
逻辑回归是一种线性模型,对于一个给定的输入向量 ,模型的输出是通过一个线性函数来预测的,然后这个线性函数的结果被sigmoid函数映射到(0, 1)区间用于二分类问题。逻辑回归模型形式如下:
逻辑回归中,每个特征都有一个对应的权重 ,这些权重独立地与相应的特征相乘,然后所有这些乘积相加,得到一个总的得分,最后通过sigmoid函数转换为概率。它并没有直接考虑特征之间的组合或交互(contact or interaction)。
决策树 (Decision Trees)
相对的,决策树是一种非线性模型,它通过一系列的问题来对数据进行分类或回归。每个内部节点代表对一个属性的测试,每个分支代表一个测试输出,每个叶节点代表一个类别。决策树直接考虑了特征之间的交互,因为一个特征的分支结果可以影响后续特征分支决定的条件。
例如,考虑一个预测个人信用评分的问题,两个输入特征:年龄(age)和年收入(income)。决策树可以先根据年龄来分枝,对于每一个年龄组,再根据年收入来进一步分枝。这样,决策树就自然地捕捉到了年龄和收入的交互作用——如果某个年龄段里,高收入可能意味着更高的信用评分,这种关系将会在决策树的路径中反映出来。
对比理解
在我们的例子中,如果使用逻辑回归,模型会评估年龄(age)和年收入(income)对信用评分的独立影响,并且需要我们手动添加交互项(如 age * income)来捕捉这两个特征的高阶关系。如果我们不这样做,逻辑回归模型可能就忽略了某些群体中年龄和收入共同作用的信息。
而决策树模型则会在树的构建过程中直接考虑到这种高阶特征关系。它通过分析特征在不同条件下的组合效果,能够直接在模型结构中展现出特征间的依赖关系。这意味着决策树在没有任何额外操作的情况下,能够自然地考虑高阶特征组合,而逻辑回归则需要我们手动设计高阶特征来实现这一点。
\[ y(\mathbf{x})=w_0+\sum_{i=1}^n w_i x_i . \]
不过,我们完全可以在逻辑回归中手动创建交互特征,比如通过组合两个特征的乘积作为新的特征引入模型,从而让模型能够考虑到特征之间的相互作用。
Poly2(Degree-2 Polynomial Margin)其实就是将多项式扩展的特征工程操作直接embedding到模型中,但是Poly2中有一个非常严重的问题就是:只有当两个特征组合项(xi和xj)均为非零值的时候,该组合特征才有意义,但是在本身就数据稀疏的业务场景中,该算法的的训练效果是不尽人意的。 \[ y(\mathbf{x})=w_0+\sum_{i=1}^n w_i x_i+\sum_{i=1}^n \sum_{j=i+1}^n w_{i j} x_i x_j \] 实际上,FM算法只是将Poly2算法中的组合特征权重转换为两个向量的内积。换句话说,针对每个特征属性都训练其对应的特征向量/隐特征向量。通过这种方式,可以解决Poly2算法特征稀疏导致模型训练完成后效果差的问题。因此,FM的主要优缺点如下:
优点:
- FM的隐向量的加入大大增强了模型的泛化能力。因为不同交叉特征中的相同特征的隐向量共享,所以不会因为数据稀疏导致隐向量的训练不充分。
- FM的时间复杂度不高,训练和推理均可以达到O(kn)(k<<n)的级别。
- 参数量减少, 使得推理的计算量减小, 而且不容易过拟合。
缺点:
- 特征和不同类型特征组合的时候只能使用同一组特征隐向量。
- 解释性不强。
为了解决大多数特征组合都为零、模型在这些高维稀疏空间中过于复杂且难以学习特征间有效的交互信息, 于是我们将\(w_{ij}\)拆解为两个向量, 用两个向量\(v_i、v_j\)的内积来近似权重\(w_{ij}\)。
那么这个时候\(v_i、v_j\)的学习就不依赖于这种组合了, 此时\(v_i\)对应的就是特征\(x_i\), \(v_j\)对应的就是特征\(x_j\)。现在我们假设\(x_i和x_j\)均为非零值时的组合不存在,现在假设两个特征间值的组合有两种\((x_i, x_k)、(x_r,x_p)\) ,那是不是就意味着\(<v_i, v_k>能从x_i、x_k所对应的特征属性中学习,<v_r, v_j>能从x_r、x_j所对应的特征属性中学习\), 这就和矩阵分解的思路有些类似了。那么此时权重\(w\)其实就表示了特征组合的重要程度, 如果\(x_i与x_j\)包含的一些隐特征时恰好匹配的,那么此时\(w_{ij}=<v_i,v_j>\)的值就会比较大, 也就是说对每一个特征属性都训练一个隐特征向量, 这样我们就不需要再考虑两两特征属性值的组合是否有意义。
举个例子,如果我们使用传统的线性模型来处理一个含有用户和商品的推荐系统问题,那么就需要为每个用户-商品对分配一个权重。考虑到用户和商品的数量可能都非常大,这将导致一个庞大的参数空间,很多用户-商品对可能从未在训练数据中出现,那么模型对这些组合的权重学习将会非常困难,且容易过拟合。
因子分解机通过引入每个特征的隐向量来解决这个问题。每个特征的交互不是直接作为一个参数被学习,而是通过学习特征的隐向量来间接学习。这样,在计算两个特征的交互时,我们不再依赖于一个特定的权重参数,而是通过这两个特征的隐向量的内积来得到。
这种方法降低了模型参数的数量,因为隐向量的维度通常远小于特征组合的数量。同时,它也让模型能够在观测到有限的特征组合的情况下,对未观测到的组合进行一定程度的泛化。理解隐向量内积作为特征交互权重的思想重点在于相似的特征将被映射到隐空间中相似的向量,因此即便没有直接观测到它们的交互,模型也能通过学习到的隐空间结构估计它们的交互效应。这是一个强大的特性,这也使得因子分解机特别适合处理高维稀疏数据集,例如推荐系统中常见的用户-物品交互。
\[
y=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^n\langle
V_i,V_j\rangle x_ix_j
\] 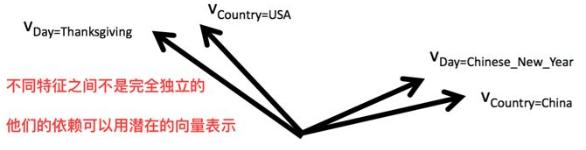
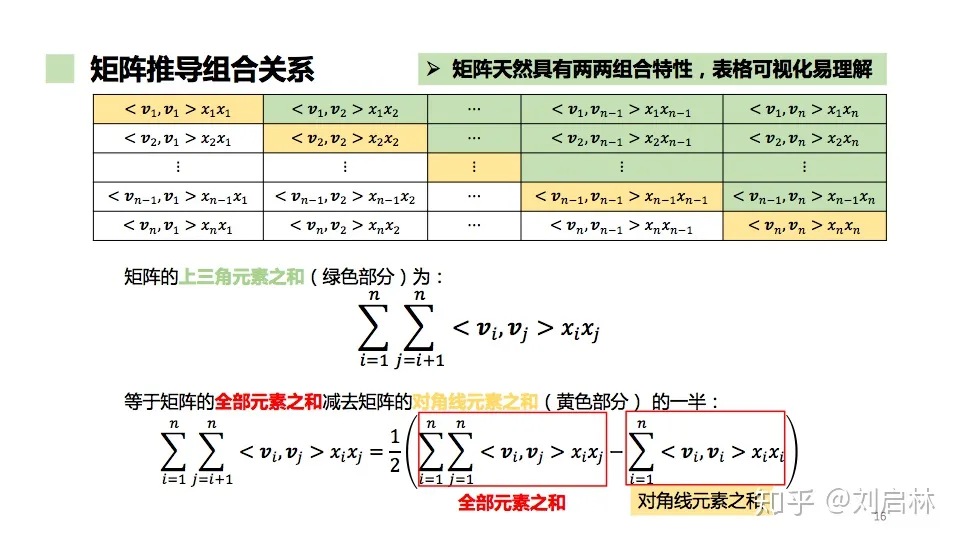 \[
\begin{aligned}
& \sum_{i=1}^{n} \sum_{j=i+1}^n\left\langle V_i, V_j\right\rangle
x_i x_j \\
= & \frac{1}{2} *\left\{\sum_{i=1}^n \sum_{j=1}^n\left\langle V_i,
V_j\right\rangle x_i x_j-\sum_{i=1}^n\left\langle V_i, V_i\right\rangle
x_i x_i\right\} \\
= & \frac{1}{2} *\left\{\sum_{i=1}^n \sum_{j=1}^n \sum_{f=1}^k v_{i
f} v_{j f} x_i x_j-\sum_{i=1}^n \sum_{f=1}^k v_{i f} v_{i f} x_i
x_i\right\} \\
= & \frac{1}{2} * \sum_{f=1}^k\left\{\sum_{i=1}^n \sum_{j=1}^n v_{i
f} x_i v_{j f} x_j-\sum_{i=1}^n v_{i f}^2 x_i^2\right\} \\
= & \frac{1}{2} * \sum_{f=1}^k\left\{\left(\sum_{i=1}^n v_{i f}
x_i\right)\left(\sum_{j=1}^n v_{j f} x_j\right)-\sum_{i=1}^n v_{i f}^2
x_i^2\right\} \\
= & \frac{1}{2} * \sum_{f=1}^k\left\{\left(\sum_{i=1}^n v_{i f}
x_i\right)^2-\sum_{i=1}^n v_{i f}^2 x_i^2\right\}
\end{aligned}
\] FM算法的训练同 \(L R\) 一样,
可以采用梯度下降的方式来更新参数, 其更新公式如下,
可以看出来,时间复杂度为 \(O(kn)\)
\[
\begin{aligned}
& \sum_{i=1}^{n} \sum_{j=i+1}^n\left\langle V_i, V_j\right\rangle
x_i x_j \\
= & \frac{1}{2} *\left\{\sum_{i=1}^n \sum_{j=1}^n\left\langle V_i,
V_j\right\rangle x_i x_j-\sum_{i=1}^n\left\langle V_i, V_i\right\rangle
x_i x_i\right\} \\
= & \frac{1}{2} *\left\{\sum_{i=1}^n \sum_{j=1}^n \sum_{f=1}^k v_{i
f} v_{j f} x_i x_j-\sum_{i=1}^n \sum_{f=1}^k v_{i f} v_{i f} x_i
x_i\right\} \\
= & \frac{1}{2} * \sum_{f=1}^k\left\{\sum_{i=1}^n \sum_{j=1}^n v_{i
f} x_i v_{j f} x_j-\sum_{i=1}^n v_{i f}^2 x_i^2\right\} \\
= & \frac{1}{2} * \sum_{f=1}^k\left\{\left(\sum_{i=1}^n v_{i f}
x_i\right)\left(\sum_{j=1}^n v_{j f} x_j\right)-\sum_{i=1}^n v_{i f}^2
x_i^2\right\} \\
= & \frac{1}{2} * \sum_{f=1}^k\left\{\left(\sum_{i=1}^n v_{i f}
x_i\right)^2-\sum_{i=1}^n v_{i f}^2 x_i^2\right\}
\end{aligned}
\] FM算法的训练同 \(L R\) 一样,
可以采用梯度下降的方式来更新参数, 其更新公式如下,
可以看出来,时间复杂度为 \(O(kn)\)
\[ \frac{\partial y}{\partial \theta}= \begin{cases}1, & \text { if } \theta \text { is } w_0(常数项) \\ x_i, & \text { if } \theta \text { is } w_i(线性项) \\ x_i \sum_{j=1}^n v_{j f} x_j-x_i^2 v_{i f}, & \text { if } \theta \text { is } v_{i f}(交叉项)\end{cases} \]
由于\(\sum_{j=1}^n v_{j f} x_j\)只与f有关, 在参数迭代过程中, 我们只需要计算一次所有的\(\sum_{j=1}^n v_{j f} x_j\)即可,显然, 计算所有f的\(\sum_{j=1}^n v_{j f} x_j\)的复杂度是O(kn)。因为我们数据集的维度是n维的, 那么当我们已知\(\sum_{j=1}^n v_{j f} x_j\)时,计算每个参数梯度的时间复杂度是\(O(n)\)。得到梯度后, 更新每个参数的复杂度是\(O(1)\); 而模型参数一共有\(nk+n+1\)个, 因此, FM参数训练的时间复杂度是\(O(kn)\)
综上可知, FM算法可以在线性时间内完成模型训练, 以及对新样本做出预测, 所以说FM是一个非常高效的模型。
总结一下:
- FM是线性模型的替代品, 能用线性回归、逻辑回归的场景都可以用FM
- FM使用了二阶交叉特征, 表达能力比线性模型更强(在推荐系统中, 交叉特征非常有用)。
- 通过做近似\(w_{ij}\approx v_i^Tv_j\), FM把二阶交叉权重的数量从\(O(n^2)\)降低到\(O(kn)\)
向量召回
 \[
y=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n\langle
V_i,V_j\rangle x_ix_j
\] 我们认为特征属性矩阵其实就两方面, 一方面是用户特征,
还有一方面是物品特征。若将FM应用于召回的话,
因为在线推理的时候用户只有一个, 物品有多个。所以对于当前用户来说,
\(w_0、\sum_{u_i \in
\text{user}}w_{u_i}*x_{u_i}\)
它们都是一个固定值,而当前用户只有一个,
所以用户与用户交叉项也是一个固定值(下图中已省略),
所以我们也可以把也给去掉。并且因为商品特征这一项\(\sum_{i_j\in \text{item}}
w_{i_j}*x_{i_j}\)与用户没有关系, 且它也是一个常数项,
只不过它是和商品相关的(不同物品值会有所不同),
但针对当前用户而言,有些情况下我们要的是近似求解,
所以我们也可以先不考虑该项
。因为召回过程我们最终需要的不是实际的置信度,
而是排好序的结果, 所以这些常数项我们就可以不考虑,
于是最后就只剩下user&item的交叉项,
于是我们就可以把我们的目标函数从:
\[
y=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n\langle
V_i,V_j\rangle x_ix_j
\] 我们认为特征属性矩阵其实就两方面, 一方面是用户特征,
还有一方面是物品特征。若将FM应用于召回的话,
因为在线推理的时候用户只有一个, 物品有多个。所以对于当前用户来说,
\(w_0、\sum_{u_i \in
\text{user}}w_{u_i}*x_{u_i}\)
它们都是一个固定值,而当前用户只有一个,
所以用户与用户交叉项也是一个固定值(下图中已省略),
所以我们也可以把也给去掉。并且因为商品特征这一项\(\sum_{i_j\in \text{item}}
w_{i_j}*x_{i_j}\)与用户没有关系, 且它也是一个常数项,
只不过它是和商品相关的(不同物品值会有所不同),
但针对当前用户而言,有些情况下我们要的是近似求解,
所以我们也可以先不考虑该项
。因为召回过程我们最终需要的不是实际的置信度,
而是排好序的结果, 所以这些常数项我们就可以不考虑,
于是最后就只剩下user&item的交叉项,
于是我们就可以把我们的目标函数从:
\[ \hat{y_i}(x)=w_0+\sum_{u_i\in user}w_{u_i}*x_{u_i}+\boxed{\sum_{i_j\in item}w_{i_j}*x_{i_j}}+\sum_{u_i\in user}\langle v_{u_i},v_{u_i}\rangle x_{u_i}^2+\sum_{i_j\in item}\langle v_{i_j},v_{i_j}\rangle x_{i_j}^2+\boxed{\sum_{u_i\in user}\sum_{i_j\in item}\langle v_{u_i},v_{i_j}\rangle x_{u_i}x_{i_j}} \] 简化为: \[ \hat{y_i}(x)=\boxed{\sum_{u_i\in user}\sum_{i_j\in item}\langle v_{u_i},v_{i_j}\rangle x_{u_i}x_{i_j}} \] 并且我们可以把\(\sum_{u_i\in user}\sum_{i_j\in \text{item}}\langle v_{u_i},v_{i_j}\rangle x_{u_i}x_{i_j}\)中用户的特征向量跟物品的特征向量给分开, 然后把所有用户的特征向量累加以及所有物品的特征向量累加,然后对整个式子进行一个转化。 \[ \begin{aligned} & \sum_{u_i \in u s e r} \sum_{i_j \in i t e m}\left\langle v_{u_i}, v_{i_j}\right\rangle x_{u_i} x_{i_j} \\ = & \sum_{u_i \in u s e r} \sum_{i_j \in i t e m}\left\langle v_{u_i} \cdot x_{u_i}, v_{i_j} \cdot x_{i_j}\right\rangle \\ = & \left\langle\sum_{u_i \in u s e r} v_{u_i} \cdot x_{u_i}, \sum_{i_j \in i t e m} v_{i_j} \cdot x_{i_j}\right\rangle \end{aligned} \]
注意, 这里的\(u_i\)是用户那块的特征, 并不是一个一个的样本, 不要和ML搞混淆了。
E.g:
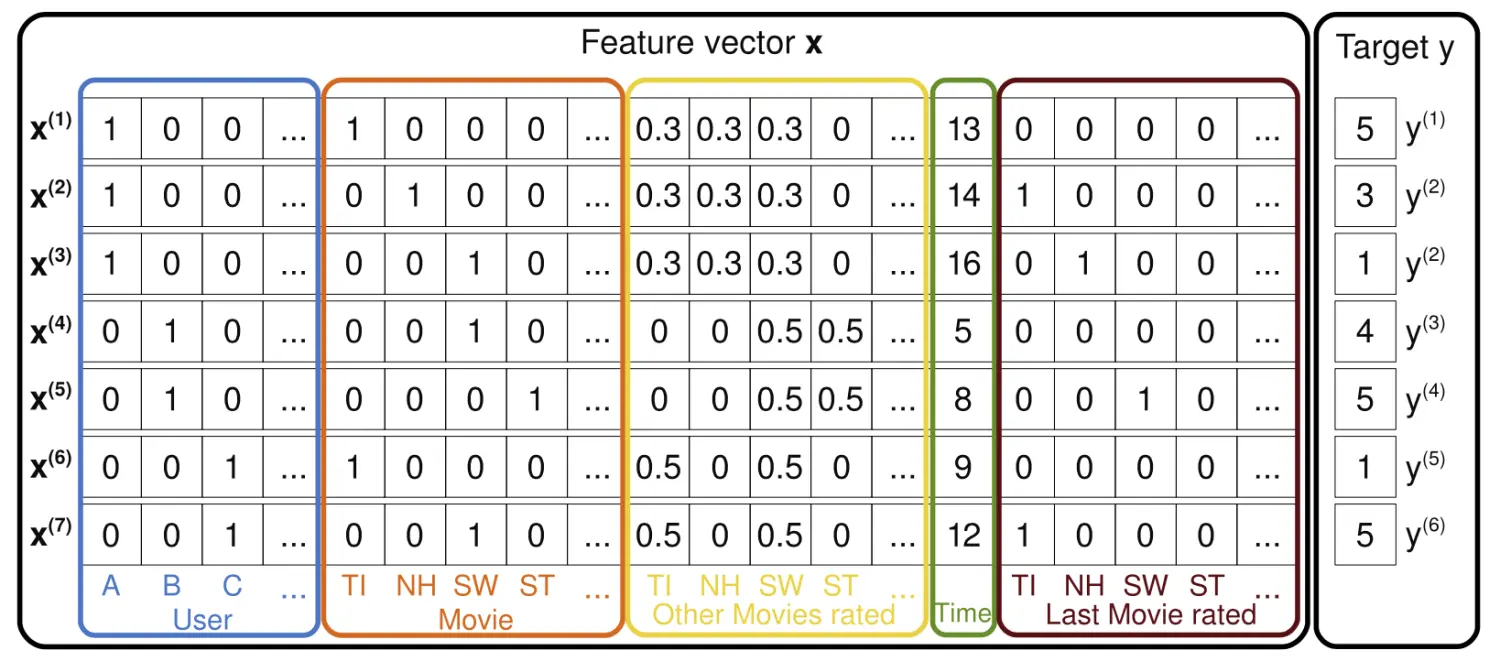
实际上一个User和一个Item对应的特征向量其实就是隐向量 \(v_i\) 和相应特征值 $x_i $相乘后所得到的一个k维的向量 。在模型训练完成后, 我们可以把所有用户和所有物品的特征向量保存到database中, 在当我们对某一用户进行商品召回的时候就可以从数据库中检索相应的用户特征向量, 然后将这个用户特征向量与所有物品的特征向量做内积(内积对应的就是余弦相似度的分子部分, 其实内积也是计算相似度的一个指标,于是我们可以根据内积的结果来计算用户和某个物品的相似度), 然后排序并将topX个物品作为召回的商品。
简单来讲User的向量和Item的向量实际上就是隐向量vi和特征值xi相乘后ui,然后将当前用户所有特征的ui相加就是当前用户的特征向量,将当前物品所有特征ui相加就是当前物品的特征向量。
如果考虑一阶特征&物物交叉特征的话,就在所有用户的特征向量上新增加一个维度, 且用户特征向量的最后一个维度的特征值为1,物品特征向量的最后一个维度的特征值就是一阶特征&物物交叉特征计算出来的常数。
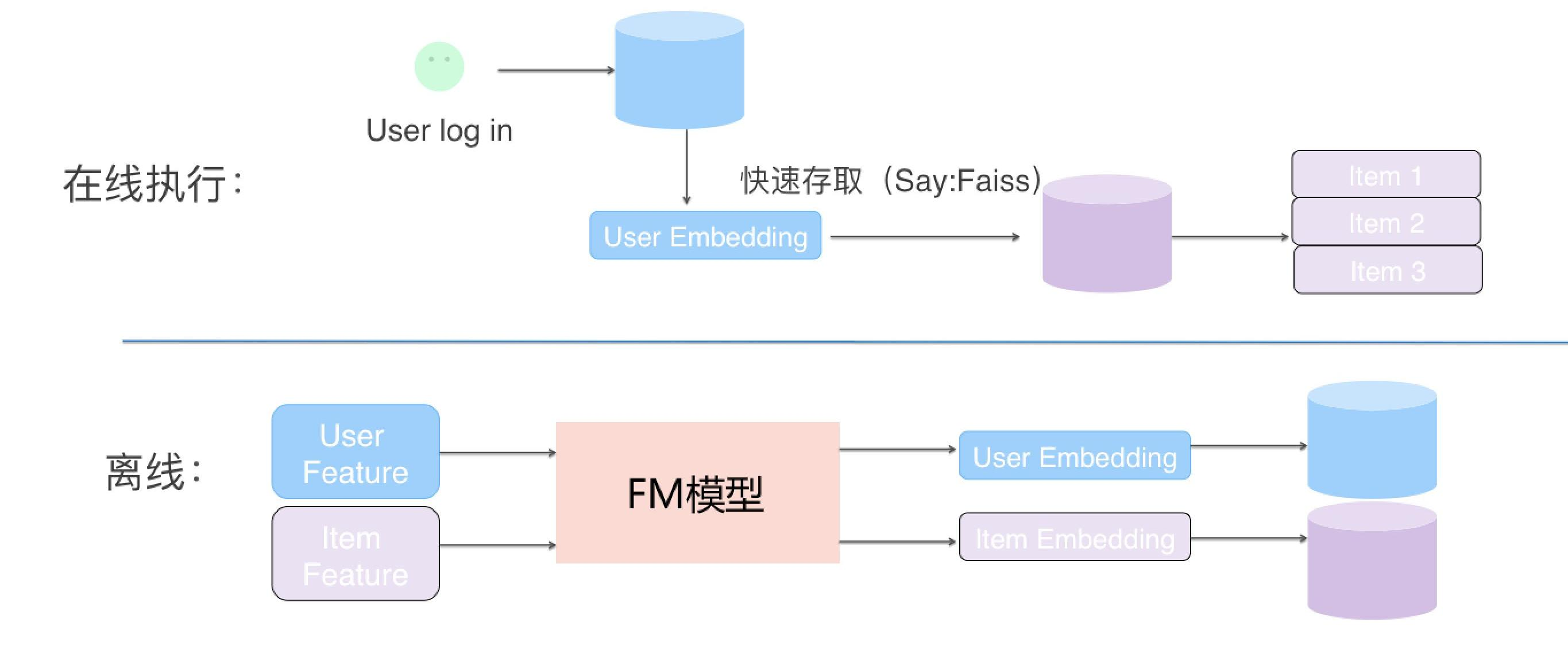
针对用户行为特征(例如用户最近点击的商品id列表),没办法离线构建好。一般采用的方式是从物品向量矩阵中提取物品向量,然后相加直接作为用户行为特征向量。最后将用户行为特征向量和用户特征向量相加作为最终的检索向量。(NOTE:用户特征向量可以在线构建)
能够解决冷启动的召回问题, 针对新用户, 直接在线调用模型计算用户特征向量即可;针对于新商品, 直接在商品录入的时候, 调用模型获取物品特征向量
如此, FM便完成了向量召回, 类似于FM这种基于用户向量和商品向量的形式其实就叫做向量召回, 而FM是向量召回中的一种, 就是我用FM来产生这个向量, 并且我也可以用其他的方式来产生这个向量。
推荐算法—FFM
在FM的基础上引入域的概念, 相当于将 \(\mathrm{n}\) 个特征属性划分为 \(\mathrm{f}\) 个域, 每个域学习一个隐向量, 这样模型的表达能力会更强, 但是由于隐向量和域相关, 也就是和特征属性相关, 所以没办法简化, FFM的时间复杂度为 \(O(k n \wedge 2), 一\) 般在稍微大一点的公司都没办法使用该模型。 \[ y(\mathbf{x})=w_0+\sum_{i=1}^n w_i x_i+\sum_{i=1}^n \sum_{j=i+1}^n\left\langle\mathbf{v}_{i, f_j}, \mathbf{v}_{j, f_i}\right\rangle x_i x_j \]
LR、FM、FMM
思考一个问题:
- 刚刚我们介绍到的LR、FM、FFM从算法论文上来讲,一般输入的特征都是离散化的类别特征(一般采用One-Hot处理)。那么如果现在存在连续特征,比如商品价格、用户年龄等,一般采用如何处理?为什么呢?
我们一般会将某些连续型数据进行分箱/分桶变成离散型的数据, 然后再做onehot。因为分桶这个操作可以解耦不同特征取值的互斥问题, 或者说耦合性。
针对问题1中的处理方式,有没有特例呢?
不是所有的连续型数据都要做分箱操作, 当某些连续型特征的取值本身就有非常重要的实际含义,例如用户对某一类商品的点击率, 这种连续型数据就不适合做分桶, 这种情况下如果再做分桶的话就会把特征之间的差异性给完全抹平。
用深度学习算法做推荐
推荐算法_Wide&Deep
Wide&Deep模型是一个线性模型与深度模型结合的产物。
wide&deep实际上就是将一个普通的全连接神经网络(单层的NN, 其实就是一个Logistic Regression)和一个深度学习模型合并后的一个model
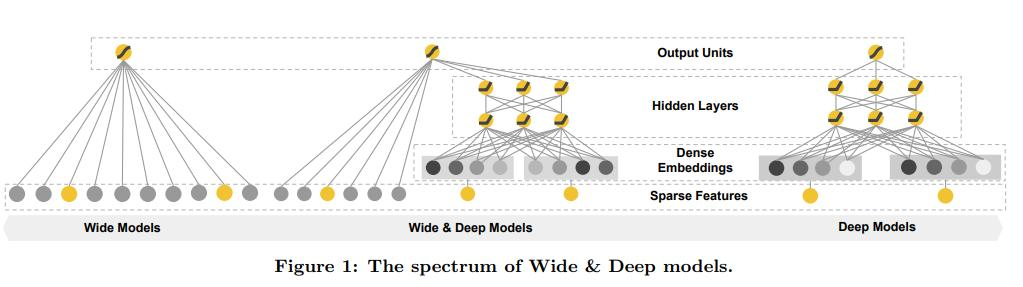
在deep model中,先将离散特征进行embedding向量化, 然后经过两个全连接层, 最后得到一个置信度。当我们把deep model的置信度与wide model得到的置信度相加, 其实就对应了中间的wide&deep model。 deep model稍微复杂一点也就是embedding+全连接mlp。 \[ P(Y=1|\mathbf{x})=\sigma(\mathbf{w}_{wide}^{T}[\mathbf{x},\phi(\mathbf{x})]+\mathbf{w}_{deep}^{T}a^{\left(l_{f}\right)}+b) \]
wide model的特征是没有做太多转换的,所以具有一个比较强的特征的记忆能力(memorization), 即保留了模型对历史数据的处理能力。
我们都知道深度学习模型有很强的数据拟合能力, 在多层神经网络中, 特征可以得到充分的交叉, 来让模型充分学习到新的知识。而deep model就因为做了很多的特征转换, 相当于提取到的是更抽象的高阶特征, 于是就让我们的模型具有了泛化能力(generalization)。而我们把这两个模型合并到一起就相当于我们的模型兼具LR和DNN的优点, 即具有针对原始数据直接处理的能力, 也具有了对泛化数据处理的能力。 即我们的模型能够快速处理并记忆大量历史行为特征, 且具有强大的表达能力
模型的记忆能力
所谓的“记忆能力”, 我们可以宽泛地理解为模型直接学习历史数据中物品或者特征的“共线频率”, 并且把它们直接作为推荐依据的能力。就像我们在电影推荐中可以发现一系列的规则,比如,看了 A 电影的用户经常喜欢看电影 B,这种“因为 A 所以 B”式的规则,非常直接也非常有价值。但这类规则有两个特点:一是数量非常多,一个“记性不好”的推荐模型很难把它们都记住;二是没办法推而广之,因为这类规则非常具体,没办法或者说也没必要跟其他特征做进一步的组合。就像看了电影 A 的用户 80% 都喜欢看电影 B,这个特征已经非常强了,我们就没必要把它跟其他特征再组合在一起。现在,我们就可以回答开头的问题了,为什么模型要有 Wide 部分?就是因为 Wide 部分可以增强模型的记忆能力,让模型记住大量的直接且重要的规则,这正是单层的线性模型所擅长的。
模型的泛化能力
“泛化能力”指的是模型对于新样本以及从未出现过的特征组合的预测能力。例如: 假设我们知道25岁的男性用户喜欢看电影A, 35岁的女性用户也喜欢看电影A。如果我们想让一个只有记忆能力的模型回答“35岁的男性喜不喜欢看电影A”这样的问题, 那么模型就无法告诉我们答案, 因为历史数据中从未出现这样的组合。
而这就体现出泛化能力的重要性了。模型有了很强的泛化能力之后,才能够对一些非常稀疏的, 甚至从未见过的情况作出尽量“靠谱”的预测。
回到刚才的例子, 有泛化能力的模型回答“35岁的男性喜不喜欢看电影A”这个问题, 它的思考逻辑可能是这样的:从第一条知识, “25岁的男性用户喜欢看电影A”中, 我们可以学到男性用户是喜欢看电影A的。从第二条知识, “35岁的女性用户也喜欢看电影A”中, 我们可以学到35岁的用户是喜欢看电影A的。拿在没有其他知识的前提下, 35岁的男性同时包含合适的年龄和和性别这两个特征,所以35岁的男性大概率也是喜欢看电影A的。
NOTE:通过Wide部分来直接"记忆"历史信息,从而达到"共现”(可以理解为某些特征组合经常出现);通过Deep部分让模型具有更高的"泛化"能力。
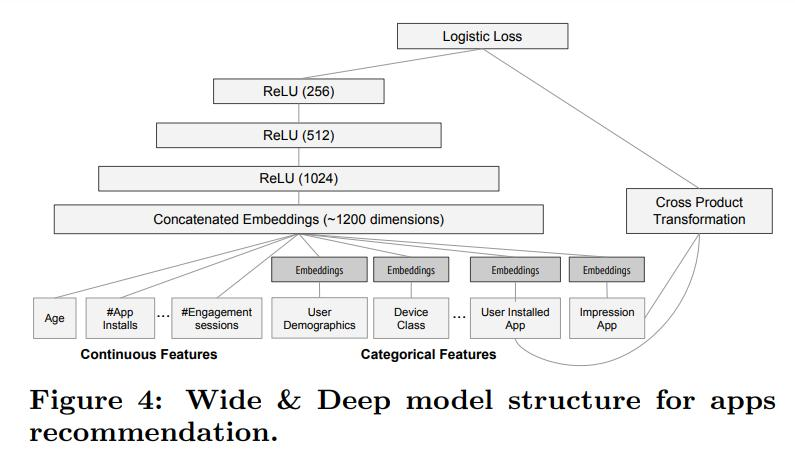
图中“已安装应用”和“曝光应用”所采用的特征都是同一种特征, 例如: 商品和商品的交叉组合、应用和应用的交叉组合。
wide 部分组合“已安装应用”和“待曝光应用”两个特征的函数被称为交叉积变换(cross product transformation)函数, 只有当安装应用i后且点击了曝光的应用j, \(x_{ij}\)才为1, 否则为0。如此一来, wide部分学到的知识就非常直观了, 就是记忆好“如果A所以B”这样的简单规则。在Google的场景下, 就是希望wide模型记住“如果用户已经安装了应用A, 是否会安装应用B”这样的规则 \[ \phi_k(\mathbf{x})=\prod_{i=1}^dx_i^{c_{ki}}\quad c_{ki}\in\{0,1\} \] 这里的\(c_{ki}\)是一个布尔型的变量,表示的是第 i 个特征的第k种转化函数的值。只有所有项都为真,最终的结果才是1,否则是0。比如"AND(gender=female,language=en)"这就是一个交叉特征,只有当用户的性别为女,并且使用的语言为英文同时成立,这个特征的结果才会是1。通过这种方式我们可以捕捉到特征之间的交互,以及为线性模型加入非线性的特征。
这种“已安装应用”和“待曝光应用”交叉的主要目的在于提高wide model 的学习能力
总的来说, Wide&Deep 通过组合Wide部分的线性模型和Deep部分的深度神经网络, 取各自所长, 就能得到一个总和能力更强的组合模型
推荐算法_Deep&Cross
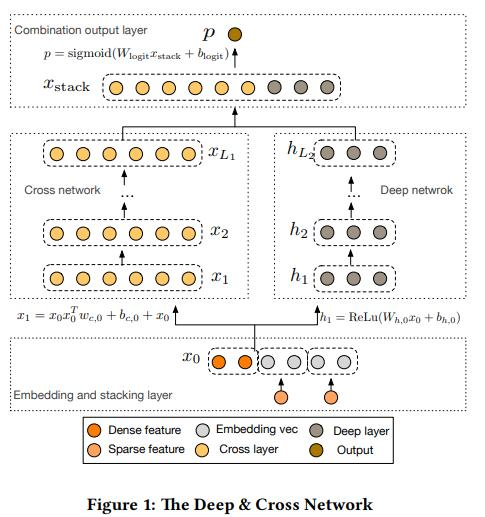
Deep&Cross(DCN)是Wide&Deep的改进版,它把Wide侧的LR换成了CrossLayer,可显式的构造 有限阶特征组合,并且具有较低的复杂度。
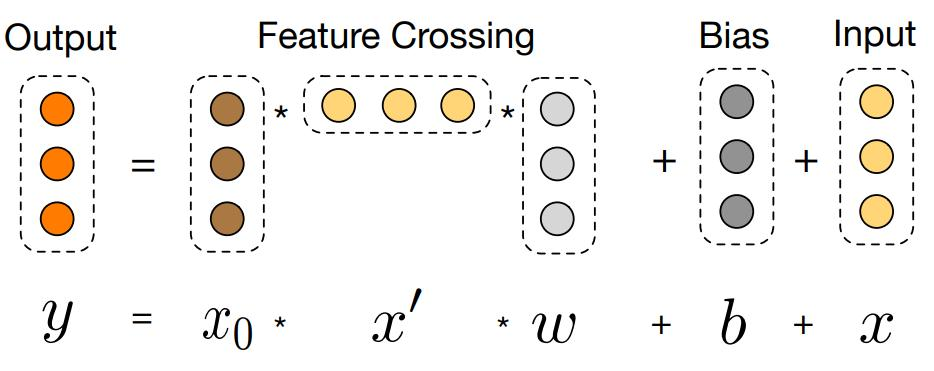
 \[
\mathbf{x}_{l+1}=\mathbf{x}_0\mathbf{x}_l^T\mathbf{w}_l+\mathbf{b}_l+\mathbf{x}_l=f(\mathbf{x}_l,\mathbf{w}_l,\mathbf{b}_l)+\mathbf{x}_l
\]
\[
\mathbf{x}_{l+1}=\mathbf{x}_0\mathbf{x}_l^T\mathbf{w}_l+\mathbf{b}_l+\mathbf{x}_l=f(\mathbf{x}_l,\mathbf{w}_l,\mathbf{b}_l)+\mathbf{x}_l
\]
深度交叉网络(DCN,Deep Cross Network)是一种有效的特征交叉方法,特别适用于高维稀疏数据。它通过跨层结构(Cross Network)显式地交叉输入特征,从而捕捉特征之间的高阶交互。
DCN的Cross Network部分实现特征交叉的方式
在DCN中,Cross Network的每一层会生成一个新的特征向量,这个向量是输入向量的线性变换与输入向量的外积(outer product)相结合的结果。具体来说,对于每一层,计算公式如下:
\(\mathbf{x}_{l+1}=\mathbf{x}_0\mathbf{x}_l^T\mathbf{w}_l+\mathbf{b}_l+\mathbf{x}_l=f(\mathbf{x}_l,\mathbf{w}_l,\mathbf{b}_l)+\mathbf{x}_l\)
举例说明
那么为什么这样设计呢? Cross究竟做了什么? 对此论文中给出了定理3.1以及相关证明,但定理与证明过程都比较烸涩,为了直观清䟷地讲解清楚,我们直接看一个具体的例子:假设Cross有2层, \(x_0=\left[\begin{array}{l}x_{0,1} \\ x_{0,2}\end{array}\right]\) ,为便于讨论令各层 \(\boldsymbol{b}_i=0\) ,则 \[ \begin{gathered} x_1=x_0 x_0^T \boldsymbol{w}_0+x_0=\left[\begin{array}{l} x_{0,1} \\ x_{0,2} \end{array}\right]\left[x_{0,1}, x_{0,2}\right]\left[\begin{array}{l} w_{0,1} \\ w_{0,2} \end{array}\right]+\left[\begin{array}{l} x_{0,1} \\ x_{0,2} \end{array}\right] \\ =\left[\begin{array}{l} w_{0,1} x_{0,1}^2+w_{0,2} x_{0,1} x_{0,2}+x_{0,1} \\ w_{0,1} x_{0,2} x_{0,1}+w_{0,2} x_{0,2}^2+x_{0,2} \end{array}\right] \end{gathered} \]
\[ \begin{aligned} x_2 & =x_0 x_1^T w_1+x_1 \\ & =\left[\begin{array}{l} w_{1,1} x_{0,1} x_{1,1}+w_{1,2} x_{0,1} x_{1,2}+x_{1,1} \\ w_{1,1} x_{0,2} x_{1,1}+w_{1,2} x_{0,2} x_{1,2}+x_{1,2} \end{array}\right] \\ & \begin{bmatrix}w_{0,1} w_{1,1} x_{0,1}^3+(w_{0,2} w_{1,1}+w_{0,1} w_{1,2} )x_{0,1}^2 x_{0,2}+w_{0,2} w_{1,2} x_{0,1} x_{0,2}^2+\left(w_{0,1}+w_{1,1}\right) x_{0,1}^2+\left(w_{0,2}+w_{1,2}\right) x_{0,1} x_{0,2}+x_{0,1} \\ \dots\end{bmatrix} \end{aligned} \]
通过类似的计算方式,可以得到包含更高阶交互的特征向量。
通过逐层的特征交叉,Cross Network可以捕捉到特征之间的高阶交互信息,并且每层的计算都是基于输入向量与前一层输出向量的交叉。这种结构使得DCN能够显式地构建特征交互,从而在处理高维稀疏数据时表现出色。
推荐算法_DeepFM
DeepFM 是 Deep 与 FM 结合的产物,也是 Wide&Deep 的改进版,只是将其中的 LR 替换成了 FM,提升了模型 Wide 侧提取信息的能力。

在Sparse Features层中, 标黄位置代表特征值为1, 灰色代表特征值为0
①是FM的一阶特征的加权求和, 因为多数特征值为0, 所以加权后的结果仍为0, 且非零特征值只为1,所以就相当于对非零元素所对应的特征的权重求和, 即①位置的三条黑线。
②是FM的二阶组合特征, 即\(\sum_{i=1}^{n}\sum_{j=i+1}^n\langle V_i,V_j\rangle x_ix_j\), 且仅当\(x_i和x_j\)非零时, 两个隐向量的内积才会有意义, 且因为Sparse Features层的特征向量中只存在0、1两种元素, 所以当\(x_i和x_j\)都有意义时\(x_ix_j=1\) 。于是\(\sum_{i=1}^{n}\sum_{j=i+1}^n\langle V_i,V_j\rangle x_ix_j\)的结果就等于特征值为非零元素对应的特征的隐向量(Embedding)之间的内积, 即\(\sum_{i=1}^{n}\sum_{j=i+1}^n\langle V_i,V_j\rangle\)
Wide&Deep:LR部分是线性模型,特征组合泛化能力有限,需要通过特征工程来增强泛化能力。 DeepFM:通过FM中的隐向量自动完成特征组合,提供泛化能力。
- 结合FM和DNN,同时学习低阶特征(FM)和高阶特征(DNN)组合;
- 端到端模型,不需要特征工程;
- 共享FM和DNN中的Feature Embedding部分,从而可以加快模型训练、互相影响促进;
因为FM中其实是有二阶交叉特征的, 所以就不需要我们做一些特征的组合了。
推荐算法_扩展
针对一组用户浏览商品id序列如何提取对应的向量(商品序列[1,3,4,5] ---> 一个128维的向量x)推荐算法扩展?
- 方案一:针对序列中的每个商品id,通过 embedding_lookup 的方式提取对应的向量(128维),然后将序列向量求均值。
- 方案二:针对序列中的每个商品id,通过 embedding_lookup 的方式提取对应的向量(128维)作为待融合的特征向量,然后再提取预测商品id对应的向量(通过 embedding_lookup 方式),将预测商品对应向量作为 Q 向量,将序列向量通过两个不同的全连接后的向量作为 K 和 V 向量,直接基于 Q、K、V 采用 attention 的思路进行向量融合。
- 方案三:在方案1基础上,对序列的 embedding_lookup 结果基于 LSTM 做一个特征的提取,将 LSTM 每个时刻的输出特征作为最终待融合的特征向量。
推荐算法_xDeepFM
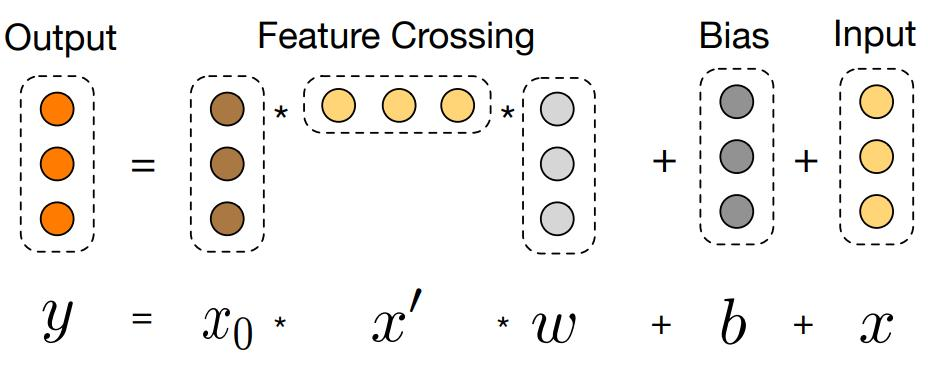
xDeepFM 是 Wide & Deep 的改进版,在此基础上添加了 CIN层(压缩感知层) 显式的构造有限阶特征组合。xDeepFM 虽然名字跟 DeepFM 类似,但是两者相关性不大(当CIN的结构退化的时候, xDeepFM就是DeepFM的泛化),DCN(Deep&Cross) 才是它的近亲。
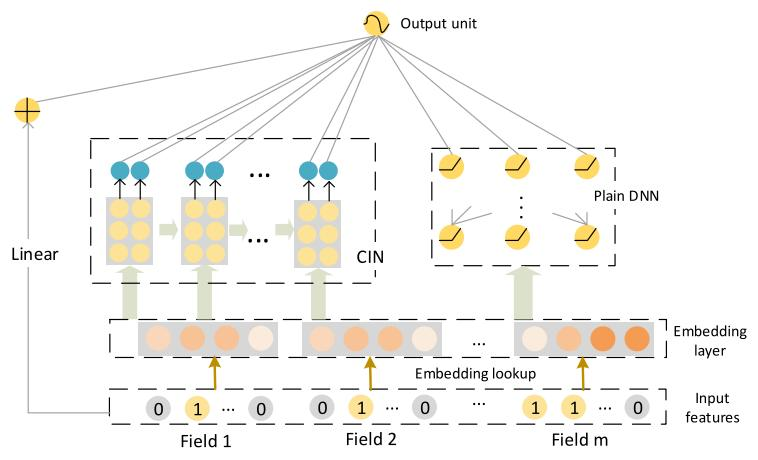
MLP结构天然就存在一种特征组合能力,但是这种组合是隐式组合(隐式的构建特征之间的交互关系:即我们不知道能够提取什么特征组合)
FM/DCN/CIN/多项式扩展:显式地进行特征与特征之间的交互
FM/CIN -- vector-wise级别的交叉特征 MLP/DCN/多项式扩展 -- bit-wise级别的交叉特征
Bit-wise特征交叉:
- 交叉方式:对每个单独维度进行交叉
- 应用场景:多项式扩展、深度交叉网络等
- 特点:直接对原始特征进行交叉,适合高维特征
Vector-wise特征交叉:
- 交叉方式:对特征对应的隐向量进行交叉
- 应用场景:FM、CIN等
- 特点:通过嵌入层将特征映射为隐向量,再进行交叉,适合稀疏特征
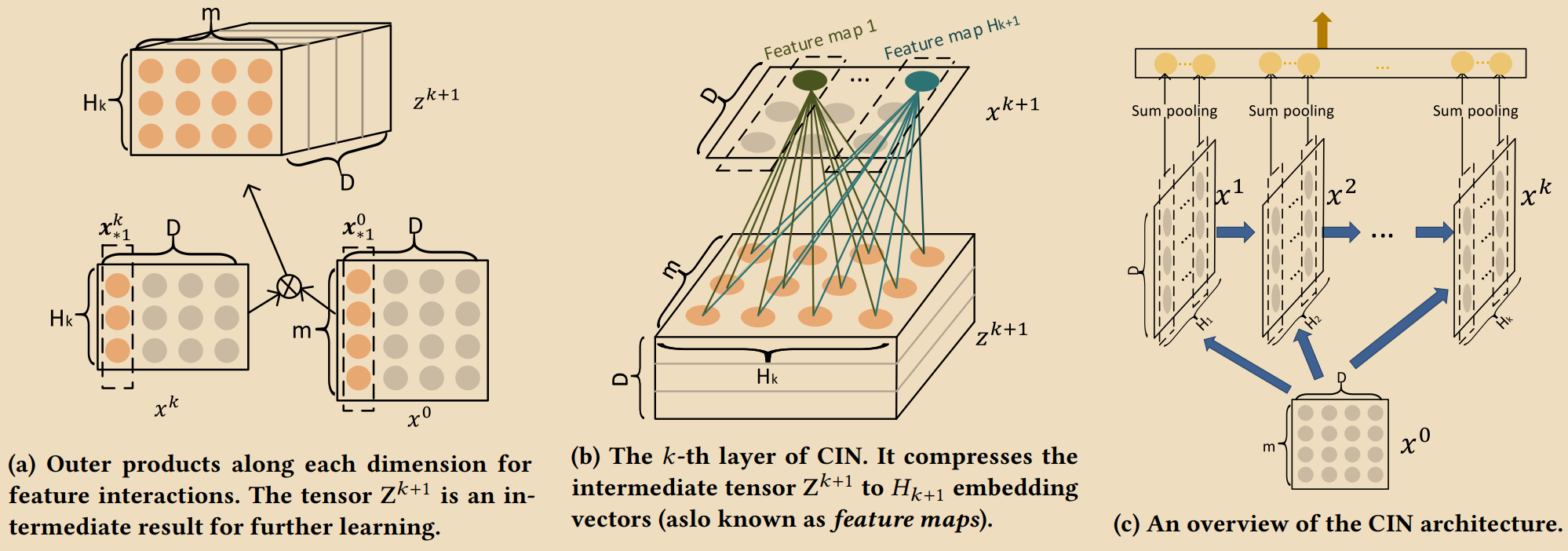 \[
\mathbf{X}_{h,*}^k=\sum_{i=1}^{H_{k-1}}\sum_{j=1}^m\mathbf{W}_{ij}^{k,h}(\mathbf{X}_{i,*}^{k-1}\circ\mathbf{X}_{j,*}^0)
\]
\[
\mathbf{X}_{h,*}^k=\sum_{i=1}^{H_{k-1}}\sum_{j=1}^m\mathbf{W}_{ij}^{k,h}(\mathbf{X}_{i,*}^{k-1}\circ\mathbf{X}_{j,*}^0)
\]
推荐算法_DSSM
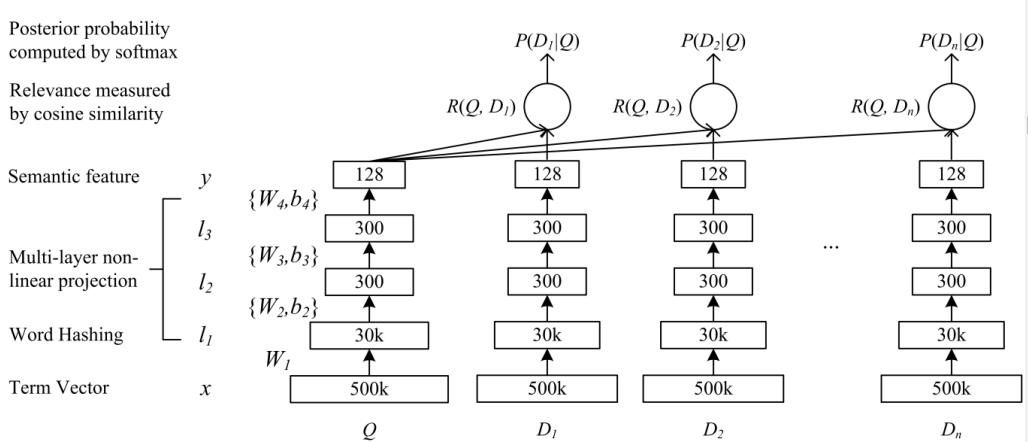
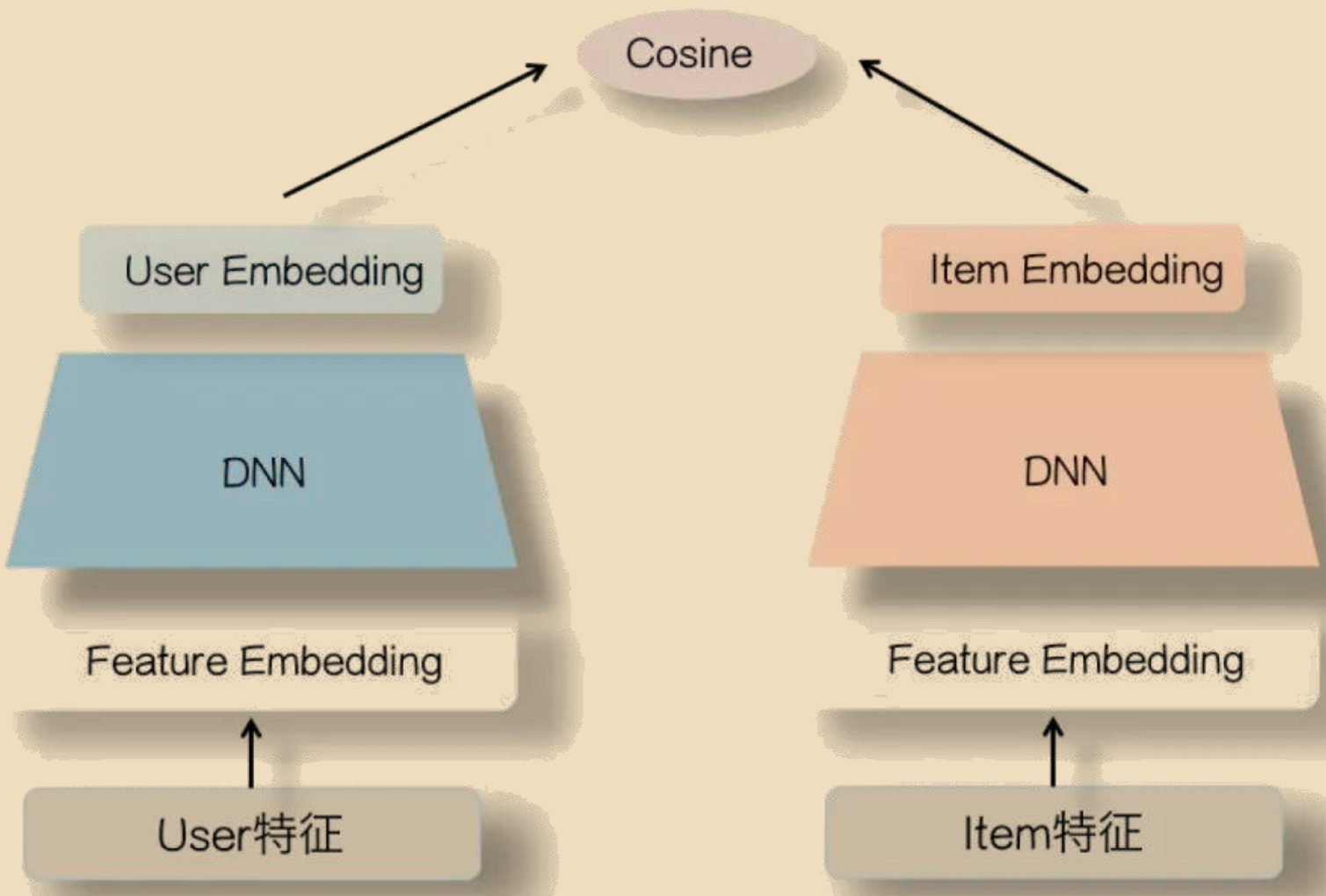
DSSM双塔模型本身是自然语言领域中文本检索的一种基础网络结构,主要用来建模每一个 query与多个documents的相似度。

推荐算法_YoutubeNet
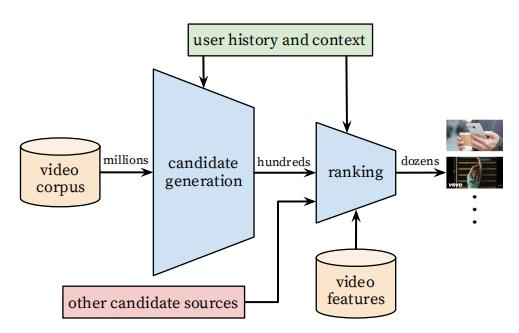
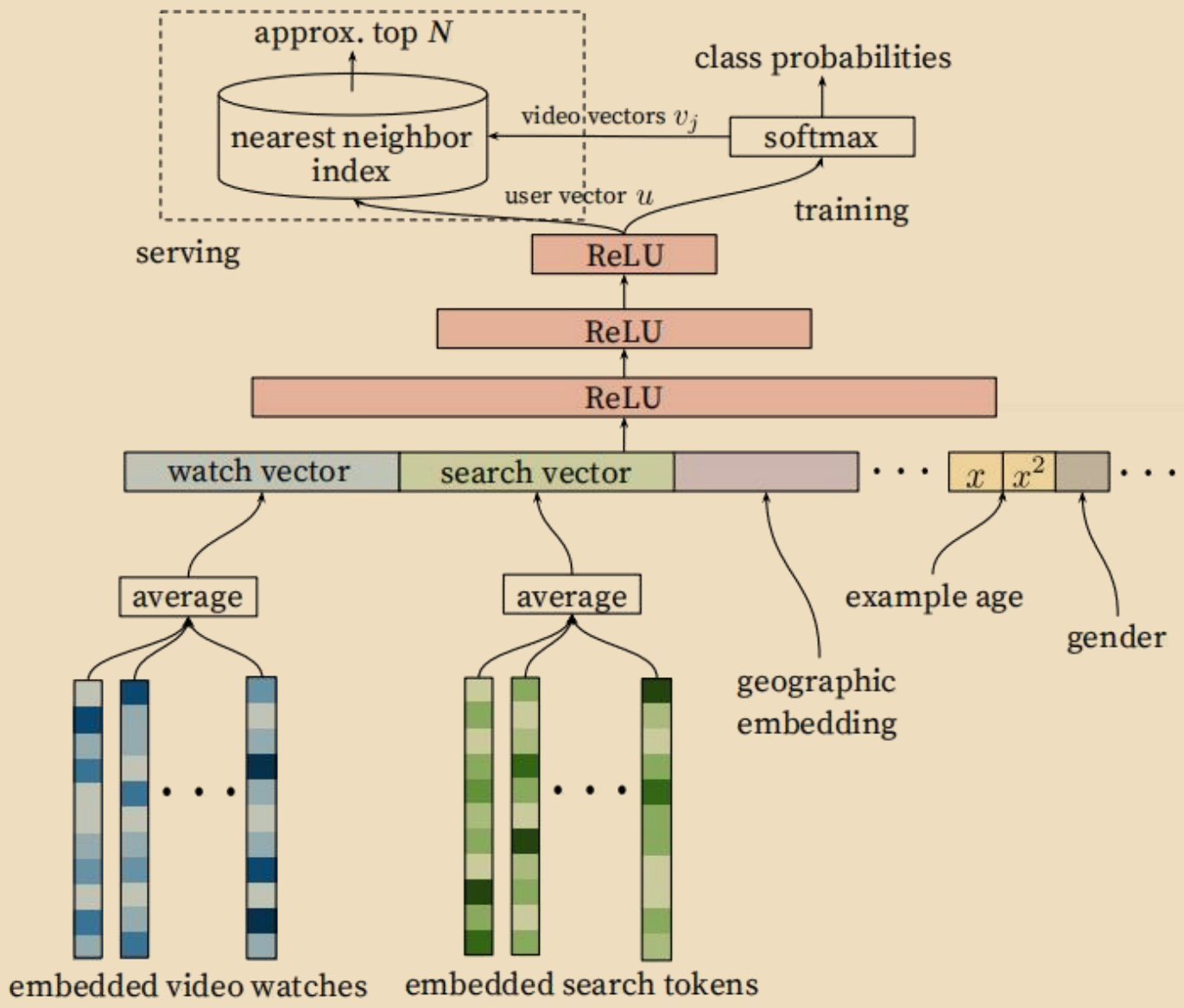
YoutubeNet是可用于召回和精排两个阶段的成熟模型,对于新视频的推荐效果非常不错。

拓展——PMML
预测模型标记语言PMML(Predictive Model Markup Language)是一套与平台和环境无关的模型表示语言,是目前表示机器学习模型的实际标准。从2001年发布的PMML1.1,到2019年最新4.4,PMML标准已经由最初的6个模型扩展到了17个模型,并且提供了挖掘模型(Mining Model)来组合多模型。
作为一个开放的成熟标准,PMML由数据挖掘组织DMG(Data Mining Group)开发和维护,经过十几年的发展,得到了广泛的应用,有超过30家厂商和开源项目(包括SAS,IBM SPSS,KNIME,RapidMiner等主流厂商)在它们的数据挖掘分析产品中支持并应用PMML,这些厂商应用详情见下表:PMML Powered
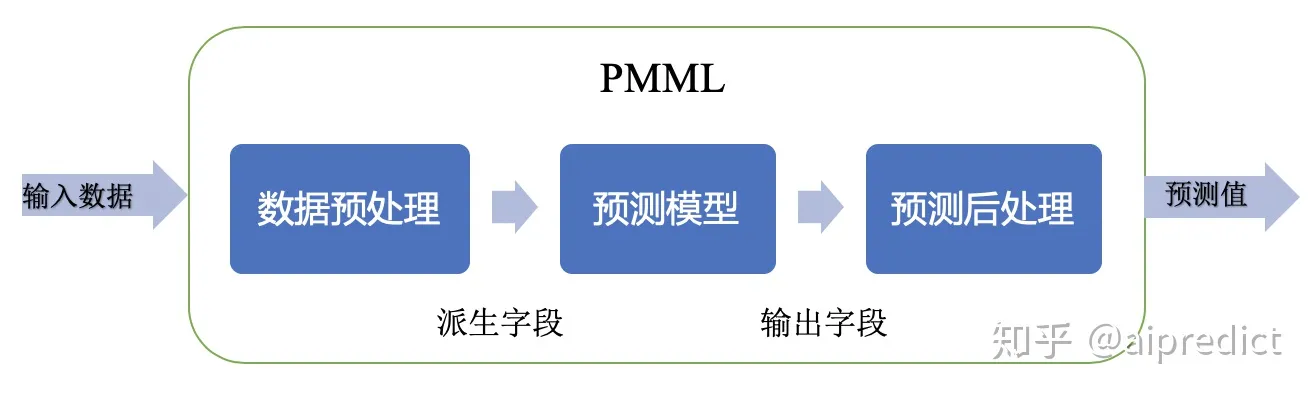
PMML标准介绍
PMML是一套基于XML的标准,通过 XML Schema 定义了使用的元素和属性,主要由以下核心部分组成:
- 数据字典(Data Dictionary),描述输入数据。
- 数据转换(Transformation Dictionary和Local Transformations),应用在输入数据字段上生成新的派生字段。
- 模型定义 (Model),每种模型类型有自己的定义。
- 输出(Output),指定模型输出结果。
PMML预测过程符合数据挖掘分析流程: