Overview of recommendation system

推荐系统概述

简单来讲就是将商品或者服务推送给用户的一种系统都可以认为是推荐系统，简单来讲可分为两种不同的系统：非个性化推荐系统(群体推荐系统)、个性化推荐系统。

个性化推荐系统和非个性化推荐系统是两种不同的信息过滤策略，它们在处理用户需求和提供内容方面有着根本的区别。

个性化推荐系统

个性化推荐系统旨在为每个用户提供定制化的内容推荐。这些系统通常基于用户的个人行为数据、历史交互、偏好设置、位置信息等来生成推荐。个性化推荐系统的关键特点包括：

• 数据驱动：使用用户的数据（如浏览历史、购买记录、评分和反馈）来生成推荐。
• 动态适应：随着用户行为的变化，推荐内容也会相应更新，以反映用户当前的兴趣和需求。
• 用户独特性：每个用户的推荐是独特的，反映了他们的个人品味和行为模式。

非个性化推荐系统

非个性化推荐系统提供标准化或统一的推荐，不考虑用户的个人差异。这类推荐通常基于整体用户数据或内容本身的属性，而不是单个用户的数据。非个性化推荐系统的关键特点包括：

• 广泛适用：推荐内容对所有用户都是一样的，例如热门商品列表、最新新闻报道等。
• 简单性：通常比个性化推荐系统更简单，因为它们不需要处理复杂的用户数据。
• 缺乏定制化：由于推荐不是基于个人用户数据，因此可能不会完全符合每个用户的独特兴趣。

应用场景

个性化推荐系统在如今的在线平台中非常常见，尤其是在电子商务、社交媒体和在线娱乐领域。它们通过提供个性化体验来增加用户的参与度和满意度。

非个性化推荐系统则可能用于新用户（没有足够历史数据的用户）、公共显示屏（如机场或购物中心的信息屏）、或者在隐私保护非常重要的场合。

推荐系统架构

image-20240506162411067

image-20240506162653502

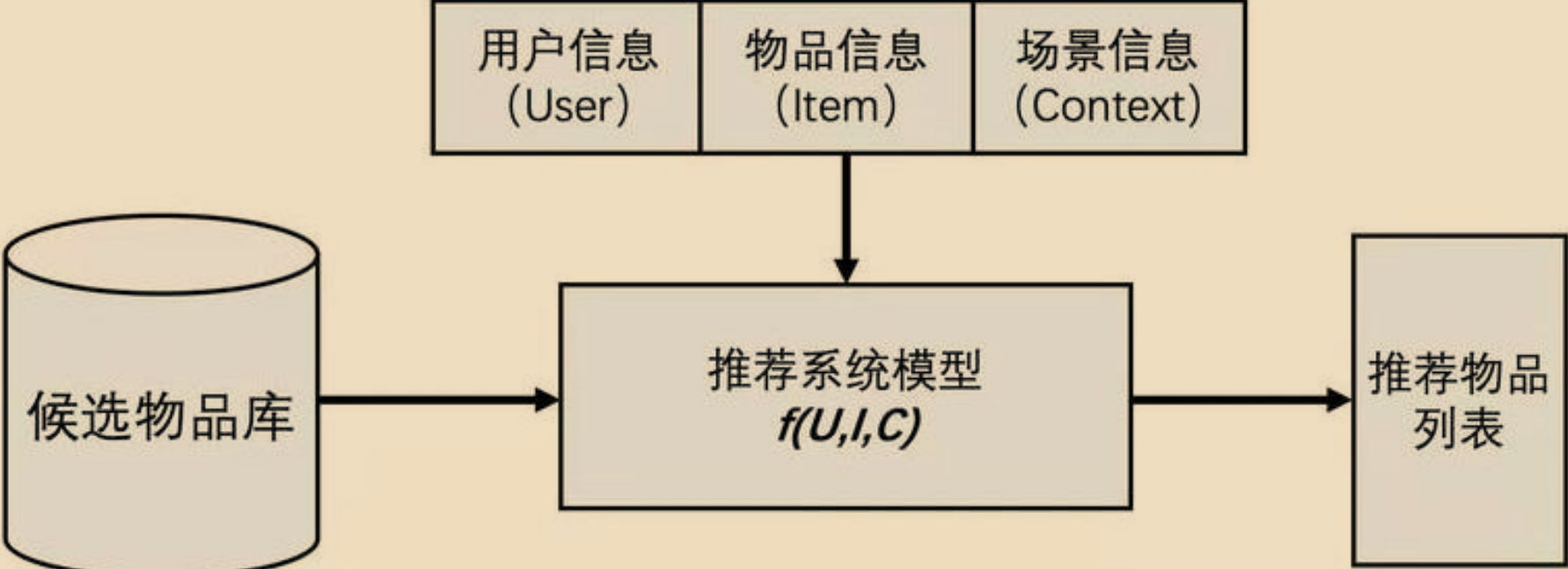
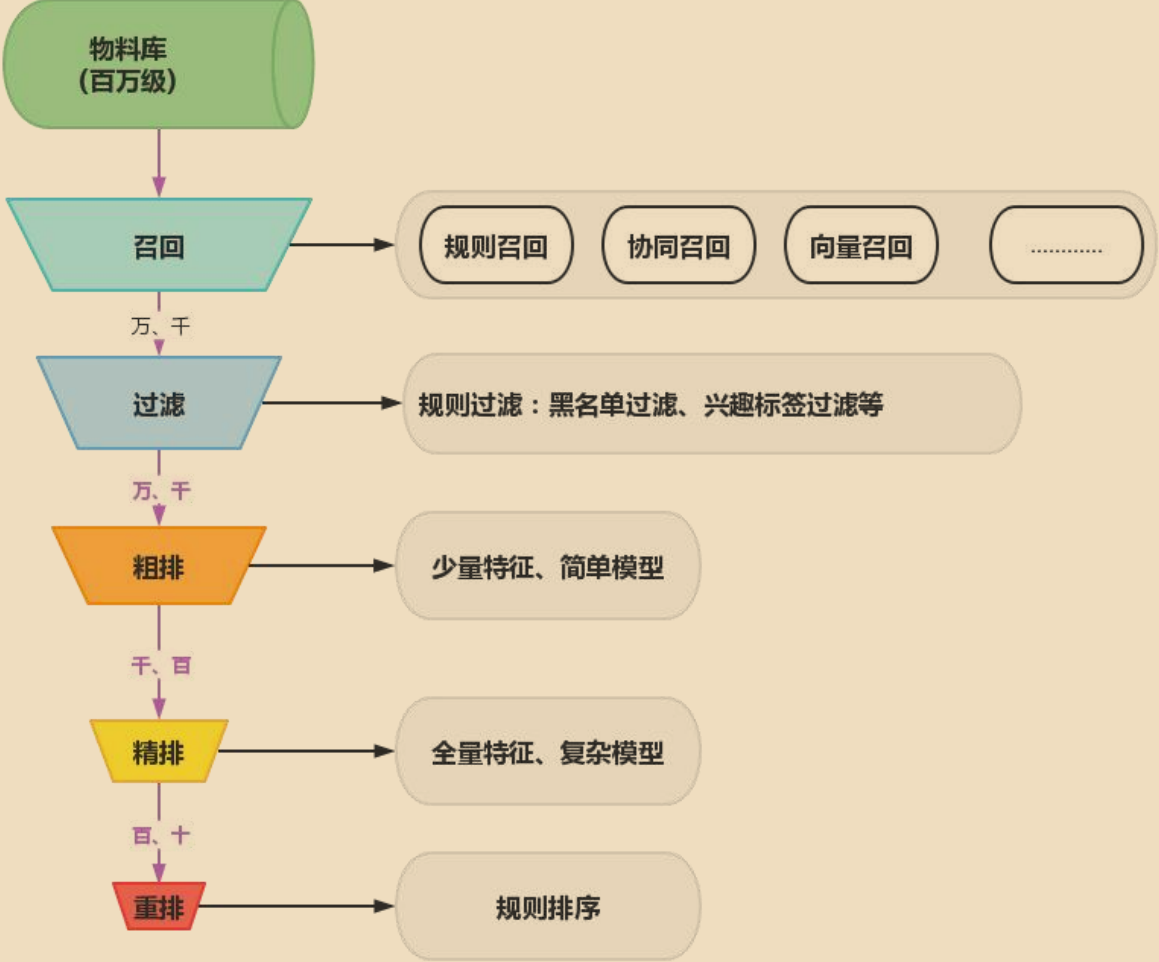
规则召回

基于规则是最常用的召回策略，也是解释性最强的召回策略。常见的规则召回策略有：基于内容标签的召回，基于商品销量或者内容热度的召回，召回历史高点击率的物料，召回平台评价&质量分比较高的物料，召回用户经常购买的一些商品或者常看的物料； Part2将会针对这一部分详细展开介绍。

此种策略的优缺点：

• 优点：策略逻辑清晰明了，业务意义明确，可解释性极强；
• 缺点：个性化弱，千人一面，为每个用户推荐的商品比较类似。同时容易引起马太效应，头部的物料得到越来越多的曝光机会，尾部的物料曝光机会越来越少。

粗排和精排

粗排（Coarse Ranking）和精排（Fine Ranking）是推荐系统中两个不同阶段的排序过程，它们在推荐流程中扮演着不同的角色。以下是它们的主要区别：

粗排（Coarse Ranking）

1. 目的：从大量的候选集中快速筛选出一小部分候选项，这些候选项被认为是相对更有可能对用户感兴趣的。
2. 算法：通常使用较为简单的模型或启发式规则，如基于用户行为的简单统计数据、热门度排序等。
3. 效率：粗排阶段强调计算效率，因为它需要处理的候选项数量非常庞大。
4. 特征：使用的特征较少，通常是高效计算的简单特征。
5. 结果：产生的是一个较大的候选项列表，但数量远小于原始的候选集。

精排（Fine Ranking）

1. 目的：在粗排选出的较小候选集基础上，进一步细化排序，以确定最终要展示给用户的Top-N项。
2. 算法：使用更复杂的机器学习模型，如梯度提升机、深度神经网络等，这些模型能够捕捉更复杂的特征间关系。
3. 效率：虽然计算成本更高，但由于处理的候选项数量较少，因此计算时间是可接受的。
4. 特征：使用更丰富的特征集合，包括用户的详细行为数据、上下文信息、个性化特征等。
5. 结果：产生的是一个精确度更高的、数量有限的推荐列表，通常是用户直接看到的推荐内容。

当物料库（即候选项集合）相对较小的时候，确实可以考虑省略粗排这个步骤。在物料库较小的情况下，直接对所有候选项进行精排（Fine Ranking）是可行的，因为：

1. 计算成本：较小的物料库意味着计算成本较低，可以直接应用复杂的机器学习模型对所有候选项进行评分和排序，而不会带来过大的计算压力。
2. 实时性：由于处理的数据量较小，可以实现更快的响应时间，即使是使用较为复杂的模型。
3. 简化流程：省略粗排步骤可以简化推荐系统的流程，减少系统的复杂性，同时避免可能由于粗排而引入的信息损失。
4. 提高准确性：直接对所有候选项进行精排可以确保不会错过任何可能对用户有高度相关性的物料。

然而，即使在物料库较小的情况下，也可能需要对推荐流程进行细致的设计，以确保推荐的相关性和多样性。此外，随着物料库的增长，可能需要重新考虑引入粗排步骤以保持系统的可扩展性和效率。因此，是否省略粗排步骤需要根据实际情况和业务需求来决定。

重排

重排的主要作用是为了提升用户的多样性体验，扶持业务产品，弥补精排的个性化不足和实现多目标的最优解。主要的策略为调权，强插，过滤，打散，多目标打分融合和模型重排。

重排是一种基于规则的排序， 这个环节一般不涉及到算法

我们再看一下上图种的结构， 在实现的时候召回这一步一般都是需要的，过滤一般也要并且它也是简单的， 然后精排一般都要， 粗排看我们的数据量如果数据量不是特别大的话粗排就可以不要了，重排看我们的业务需求， 如果我们有这样的业务需求那么我们就排序， 刚刚讲了重排其实就是业务规则， 很简单。

image-20240506162530093

拓展——“埋点与无埋点”

1. 什么是埋点

埋点，也有称打点， 顾名思义就是借助埋点（写代码）来采集数据，在需要监测用户行为数据的地方加上一段代码。我们可以称之为 Capture 模式，通过在客户端/服务端埋下确定的点，采集相关数据到云端，最终在云端做呈现。

经过数据校验后的埋点数据非常准确，稳定性高，适合监控和分析，对于非探索式分析来说是一个非常行之有效的方法；且埋点往往可以添加较多的业务属性，方便产品经理对事件进行业务属性拆解和下钻分析，能很好地从业务逻辑切入行为分析，理解行为背后的业务思路。

2. 什么是无埋点

无埋点，事实上并不是真正的不需要写代码，而是前端自动采集全部事件并上报所有的数据，并通过「圈选」来获取需要使用的事件。区别于上文埋点中提到的 Capture 模式，无埋点采用的是 Record 模式，用机器来替代人的经验。

image-20240506162643460

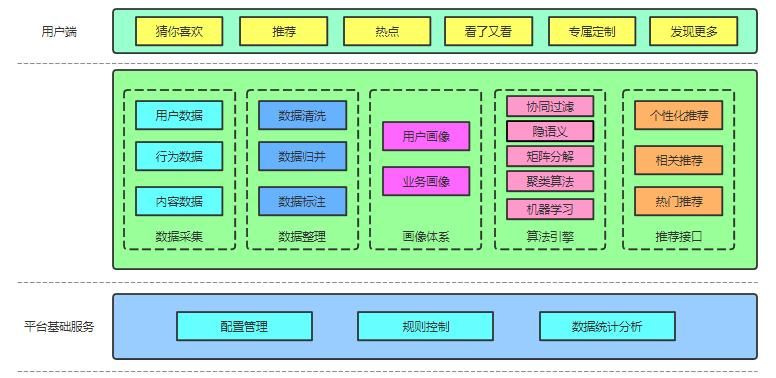
我们做推荐都是跟图中算法引擎、推荐接口这两块打交道， 其他块属于大数据、nlp、数据挖掘等方面的工程师

image-20240506162633770

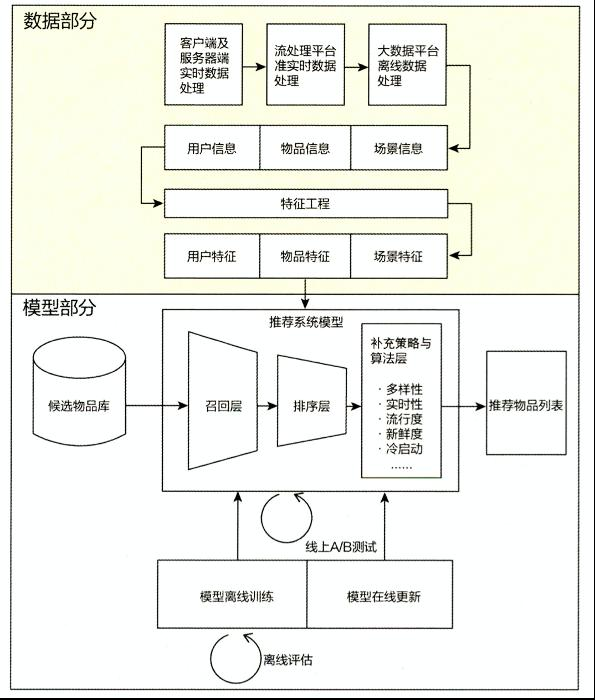
数据部分

推荐系统的数据部分（上图的上半部分所示）主要负责“用户”“物品”“场景”的信息收集与处理。具体地讲，将负责数据收集与处理的三种平台按照实时性的强弱排序，依次为“客户端及服务器端实时数据处理”、“流处理平台准实时数据处理”、“大数据平台离线数据处理”。在实时性由强到弱递减的同时，三种平台的海量数据处理能力则由弱到强。因此，一个成熟的推荐系统的数据流系统会将三者取长补短，配合使用。

在得到原始的数据信息后，推荐系统的数据处理系统会将原始数据进一步加工，加工后的数据出口主要有三个：

1. 生成推荐模型所需的样本数据，用于算法模型的训练和评估。
2. 生成推荐模型服务（model serving）所需的“特征”，用于推荐系统的线上推断。
3. 生成系统监控、商业智能（Business Intelligence，BI）系统所需的统计型数据。

可以说，推荐系统的数据部分是整个推荐系统的“水源”，只有保证“水源”的持续、纯净，才能不断地“滋养”推荐系统，使其高效地运转并准确地输出。因为数据部分通常是偏大数据的， 所以这一块通常不归我们管， 我们只需要从关系型数据库中获取大数据层面的工程师处理好的数据即可， 模型部分的任务才是真正属于我们的。

模型部分

推荐系统的“模型部分”是推荐系统的主体（如图1-4中浅蓝色部分所示）。模型的结构一般由“召回层”、“排序层”、“补充策略与算法层”组成。

• “召回层”一般利用高效的召回规则、算法或简单的模型，快速从海量的候选集中召回用户可能感兴趣的物品。
• “排序层”利用排序模型对初筛的候选集进行精排序。
• “补充策略与算法层”，也被称为“再排序层”，可以在将推荐列表返回用户之前，为兼顾结果的“多样性”“流行度”“新鲜度”等指标，结合一些补充的策略和算法对推荐列表进行一定的调整，最终形成用户可见的推荐列表。

从推荐模型接收到所有候选物品集，到最后产生推荐列表，这一过程一般称为模型服务过程。在线环境进行模型服务之前，需要通过模型训练（model training）确定模型结构、结构中不同参数权重的具体数值，以及模型相关算法和策略中的参数取值。模型的训练方法又可以根据模型训练环境的不同，分为“离线训练”和“在线更新”两部分，其中：离线训练的特点是可以利用全量样本和特征，使模型逼近全局最优点；在线更新则可以准实时地“消化”新的数据样本，更快地反映新的数据变化趋势，满足模型实时性的需求。

除此之外，为了评估推荐模型的效果，方便模型的迭代优化，推荐系统的模型部分提供了“离线评估”和“线上A/B测试”等多种评估模块，用得出的线下和线上评估指标，指导下一步的模型迭代优化。

以上所有模块共同组成了推荐系统模型部分的技术框架。模型部分，特别是“排序层”模型是推荐系统产生效果的重点，也是业界和学界研究的重心。因此在后面的章节中，笔者将着重介绍模型部分，特别是“排序层”模型的主流技术及其演化趋势。

线上A/B测试

A/B 测试又称为“分流测试”或“分桶测试”，是⼀个随机实验，通常 被分为实验组和对照组。在利⽤控制变量法保持单⼀变量的前提下， 将A、B两组数据进⾏对⽐，得出实验结论。具体到互联⽹场景下的算法测试中，可将⽤户随机分成实验组和对照组，对实验组的⽤户施以新模型，对对照组的⽤户施以旧模型，⽐较实验组和对照组在各线上评估指标上的差异。

在推荐系统中，rating和ranking是两个建模方向：

1. Rating：
   • 指构建模型预测用户对商品的评分，然后基于同一用户在不同物品上的评分大小，提取评分最高的商品序列作为推荐列表。
2. Ranking：
   • 指直接构建模型预测用户对商品的推荐序列，但在模型内部不关注rating评分值。
   • 相比于rating方式，ranking具有以下优点：
     • 在一些业务场景中只有ranking没有rating。
     • 对于一些业务场景来说，rating的拟合非常困难，而针对ranking拟合相对来说更容易。

需要注意的是，现阶段来讲，在推荐领域更多地使用ranking排序模型的策略。

在构建用于预测用户对商品评分的模型时，一个至关重要的前提是：训练集中必须包含足够多的用户评分数据。然而，值得注意的是，并非所有网站都拥有充足的用户评分数据。那么是否使用rating则需要打一个问号。事实上，有些网站可能没有足够的用户评分数据，或者并不是所有用户都会留下评分。

此外，对于某些业务场景，特别是那些需要对序列数据进行建模的场景，实现准确的模型拟合可能会非常具有挑战性。与此相对的是，基于排名的模型通常更容易实现。在这种情况下，简单地处理序列往往更为直接。目前，许多基于排序的模型主要依赖于项目的排名来构建，这种方法通常比尝试准确拟合用户的评分或评论行为要简单得多。

总的来说，在构建预测模型时，认真考虑数据的可用性和模型的适用性是非常重要的。优化模型性能的一个关键策略是选择一个合适的建模方法，同时充分考虑到数据的实际情况和业务需求。这也是推荐领域为什么更多地使用ranking的原因。

推荐系统的评估

MSE(均方误差)：Mean Squared Error；是指估计值与真实值之差平方的期望值。 RMSE(均方根误差): Root Mean Squared Error；是均方误差的算法平方根。 \[M S E=\frac{1}{|R|} \sum_{r_{u, i} \in R}\left(\hat{r}_{u, i}-r_{u, i}\right)^2 \quad R M S E=\sqrt{M S E}=\sqrt{\frac{1}{|R|} \sum_{u, i, R}\left(\hat{r}_{u, i}-r_{u, i}\right)^2}\] 召回率(Recall)：在推荐列表中，用户实际点击商品和用户所有点击商品之间的占比情况； 精确率(Precision)：在推荐列表中，用户实际点击的商品占比；

在排序模型中，通常没有⼀个确定的阈值把预测结果直接判定为 正样本或负样本，⽽是采⽤Top N排序结果的精确率（Precision@N）和 召回率（Recall@N）来衡量排序模型的性能，即认为模型排序的Top N的结果就是模型判定的正样本，然后计算Precision@N和Recall@N。

\[\begin{array}{|c|c|c|} \hline & \text { 实际点击列表 } & \text { 实际未点击列表 } \\ \hline \text { 推荐列表 } & \begin{array}{c} \text { TP } \\ \text { 推荐并且实际点击 } \end{array} & \begin{array}{c} \text { FP } \\ \text { 推荐但实际未点击 } \end{array} \\ \hline \begin{array}{l} \text { 未推荐列 } \\ \text { 表 } \end{array} & \begin{array}{c} \text { FN } \\ \text { 实际点击但未推荐 } \end{array} & \begin{array}{c} \text { TN } \\ \text { 实际未点击也未推荐 } \end{array} \\ \hline \end{array}\]

\[Recall=\frac{TP}{TP+FN}\ \ \ \ \ Precision=\frac{TP}{TP+FP}\]

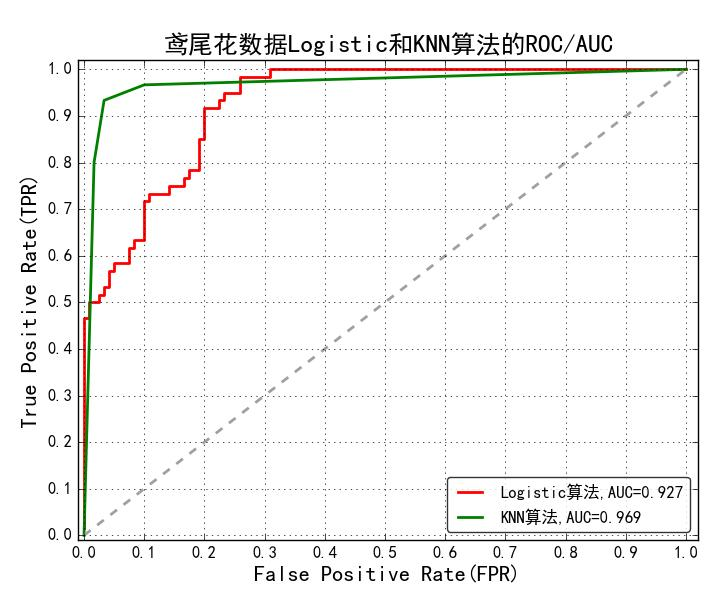
ROC曲线：

• 使用假正例率(FPR)作为横坐标，真正例率(TPR)作为纵坐标，是一种分类算法模型性能的评估方式，是一个非递减曲线。

AUC：

• 由于ROC曲线评估模型不太直观，因此采用ROC曲线下的面积作为评估指标，即AUC。AUC越大表示模型的区分能力越强，效果越好（在足够小的FPR情况下可以保证有较大的TPR）。

image-20240506164145481

MAP(平均精度均值；Mean Average Precision)

• MAP是对精准率的一个修正， 因为precision这个评价指标是对推荐顺序不敏感的。

\[\begin{aligned} & A P @ u=\frac{\sum_{N=1}^{|\widehat{R}|} \text { Precision@N } \times \operatorname{rel}(N)}{|\widehat{R}|} \\ & M A P=\frac{\sum A P @ u}{|U|} \end{aligned}\]

\(AP@u\)指的是第u个用户的AP值, \(|\hat{R}|\)是相关项的数量， 其中， 推荐列表中Top N排序结果的精确率（Precision@N）， \(\operatorname{rel}(N)\) 是一个指示函数（推荐列表中第N个推荐推荐是否是相关的，即列表中第N个推荐项目是否是用户感兴趣的内容。 如果第 \(\mathrm{N}\) 个推荐是相关的，则为 1 ，否则为 0 。并且我们也可以采用推荐的商品列表在用户实际点击列表中所处的顺序的倒数）。MAP是对所有用户的AP值的平均，其中公式中的 \(U\) 是用户的总数。

重要性

• 位置敏感性：MAP考虑了相关推荐的位置，排名越靠前的相关推荐对MAP的贡献越大。这意味着推荐系统不仅要能够找到相关的项目，还要能够将它们排在列表的前面。
• 平均性能：通过计算所有用户的AP的平均值，MAP提供了一个衡量推荐系统整体性能的指标。

MAP 可被视为精确率的一种改进或扩展，特别是在考虑到推荐或检索结果的顺序时。在推荐系统和信息检索领域，不仅重视推荐内容的相关性，还强调将最相关的内容排在尽可能前的位置。这是因为用户在查看推荐列表时，往往只关注最前面的几项。因此，推荐系统的一个关键目标是确保最相关、最有价值的项目能够获得更高的可见性。

精确率是评估模型在所有被检索或推荐的项目中，有多少是相关的。而精确率的一个局限性就是它不考虑推荐项目的顺序。无论相关项目是排在列表的第一位还是最后一位，对精确率的计算都没有影响。而MAP通过考虑推荐列表中相关项目的排名来解决这个问题。它通过计算每个相关项目被检索时的精确率，并对这些精确率值取平均，从而得到平均精确率（AP）。然后，对所有用户的AP值取平均，得到MAP。这样，MAP就能够反映出推荐系统在将相关项目排在前面方面的效能。

因此，MAP是一个更全面的评估指标，它不仅衡量了推荐系统识别相关项目的能力，还考虑了这些相关项目在推荐列表中的位置。通过优化MAP，推荐系统可以更有效地满足用户的需求，提高用户的满意度和互动率。这就是为什么在推荐系统的评估中，MAP比单纯的精确率更受青睐。

Sure, here is the text converted into a Markdown table format:

表格1

实际点击 商品列表	推荐商品 列表	Precision @ N	rel(N)
2	2	1 / 1	1
3	3	2 / 2	1
5	1	2 / 3	0
8	4	2 / 4	0
9	6	2 / 5	0

实际点击 商品列表	推荐商品 列表	Precision @ N	rel(N)
1	8	0 / 1	0
3	7	0 / 2	0
4	2	1 / 3	1
6	1	2 / 4	1
2	9	2 / 5	0

\[\begin{aligned} & A P_1=\frac{1}{5} *\left(\frac{1}{1} * 1+\frac{2}{2} * 1+\frac{2}{3} * 0+\frac{2}{4} * 0+\frac{2}{5} * 0\right)=\frac{2}{5} \\ & A P_2=\frac{1}{5} *\left(\frac{0}{1} * 0+\frac{0}{2} * 0+\frac{1}{3} * 1+\frac{2}{4} * 1+\frac{2}{5} * 0\right)=\frac{1}{6} \\ & M A P=0.5 *\left(\frac{2}{5}+\frac{1}{6}\right)=\frac{17}{60} \end{aligned}\]

NDCG

• NDCG(Normalized Discounted Cumulative Gain)：类似MAP的一种考虑序列位置的一种推荐、 搜索领域评估指标。

\[\begin{aligned} & C G @ k=\sum_{i=1}^k r e l_i \\ & D C G @ k=\sum_{i=1}^k \frac{2^{r e l_i}-1}{\log _2(i+1)} \\ & N D C G @ k=\frac{D C G @ k}{I D C G @ k} \end{aligned}\]

\(C G @ k\)是把top k个推荐项目的置信度全部加起来， 它没有考虑位置关系。\(C G @ k\)可以把哪个推荐列表好给体现出来， 它更关注用户实际点击列表中比较靠前项目。

\(DCG@k\) 是基于前 \(k\) 个推荐项的累积增益，考虑了每个项的相关性等级和位置。对于位置i的推荐项，其贡献被折扣 (discounted) 并加入到总增益中。\(D C G @ k\) 是有考虑位置关系的， 它相当于把置信度做一个转换再加起来， 但因为它没有大小范围， 因此不太好评估。所以为了评估方便, 我们就除以一个最大值（最大可能值、最大\(D C G @ k\)、最理想值）\(I D C G @ k\)， 于是得到\(N D C G @ k\)

为什么需要\(I D C G @ k\)

IDCG@k 用于标准化DCG@k，使得NDCG@k 的值在0到1之间，其中1代表完美的排序。这种标准化是必要的，因为不同的查询或推荐请求可能有不同数量的相关项，或者相关项的相关性等级分布不同，这使得直接比较不同查询的DCG@k值变得困难。通过将DCG@k除以IDCG@k，我们得到了一个归一化的指标，可以在不同的查询和推荐系统之间进行公平的比较。

NDCG@k的计算分为三个步骤:

1. 计算DCG@k (Discounted Cumulative Gain at rank k) :

\[\text { DCG } @ \mathrm{k}=\sum_{i=1}^k \frac{2^{r e l_i}-1}{\log _2(i+1)}\]

2. 计算理想的DCG@k (IDCG@k， Ideal DCG at rank k) : IDCG@k是在理想情况下 (即推荐项按照相关性等级完美排序) 的DCG@k值。它通过将相关性等级最高的项排在前 \(k\) 位来计算。
3. 计算NDCG@k: NDCG@k是DCG@k相对于IDCG@k的比值，用于标准化DCG@k，使其值在 0 到 1之间。

\[\begin{array}{ccccc} \hline \begin{array}{c} \text { 实际点击商品顺 } \\ \text { 序列表 } \end{array} & \text { 推荐商品列表 } & \text { rel\_i } & \boldsymbol{\operatorname { log }}_{\mathbf{2}}(\boldsymbol{i}+\mathbf{1}) & \boldsymbol{r e l}_{\boldsymbol{i}} / \log _{\mathbf{2}}(\boldsymbol{i}+\mathbf{1}) \\ \hline \text { p9 } & \text { p2 } & 1 / 3 & 1 & 1 / 3 \\ \text { p1 } & \text { p3 } & 0 & 1.58 & 0 \\ \text { p2 }& \text { p5 } & 0 & 2 & 0 \\ & \text { p8 } & 0 & 2.32 & 0 \\ & \text { p9 } & 1 & 2.58 & 0.38 \\ \hline \end{array}\]

这里的rel_i跟刚才的rel（N）的计算方式不太一样， 就比如rel_i=1/3时对应的推荐商品就是p2， 而p2对应的实际点击商品顺序列表的第3个位置， 我们对位置信息取一个倒数就得到rel_i的值， 所以NDCG中rel_i的计算就是推荐列表中的某一项在用户实际点击商品列表中的位置的倒数。并且这里的rel_i只和实际点击商品顺序列表有关。

\[\begin{aligned} &CG@5=(1/3+0+0+0+1)=4/3 \\ &DCG@5=(1/3+0+0+0+0.38)\approx0.71 \\ &IDCG@5=\left(1+\begin{matrix}\frac{0.333}{1.58}\end{matrix}+0+0+0\right)\approx1.21 \\ &NDCG@5=\begin{matrix}\frac{0.71}{1.21}\end{matrix}\approx0.587 \end{aligned}\]

在本例中， 最优的推荐列表应该是\(p9, p2, p...\), 推荐商品列表中包含用户实际点击的商品只有两个， 我们只需保证这两个推荐顺序最优， 剩下三个无论怎么排列都行。

有的时候, 如果我们需要考虑序列的一些影响，我们其实就要用到MAP或者NDCG，MAP与NDCG都相对要复杂一些，所以实际情况下， 我们使用更多的一个评估指标其实还是AUC。

排序模型

推荐系统的排序模型从实现思路来讲，主要是：单点法(Pointwise Approach)、配对法(Pairwise Approach)、列表法(Listwise Approach)；这三种思路的主要区别体现在损失函数、标签标注方式以及优化方法的不同。

image-20240506165502146

单点法（Pointwise）

单点法（Pointwise）是最常见的一种建模思路，该思路的主要特征如下：

• 不考虑同一个推荐序列中商品与商品之间的相关性，直接将排序问题转换为分类、回归问题，这样就可以直接使用常规的机器学习、深度学习算法来建模了；
• 模型复杂度相比Pairwise和Listwise最低；
• 数据标注简单，可直接使用用户的点击反馈等信息；
• 主要缺点就是没有考虑同推荐序列中商品与商品之间的相关性，从而导致最终模型无法学习到同品类商品与商品之间的顺序。比如：实际推荐商品评分序列为[4.5, 4.0, 3.5, 2,2,2,2,1]，通过单点法模型预测该序列对应评分为:[3.9, 4.1, 4.0, 2,2,2,2,1]，从回归模型RMSE损失来讲，实际上的损失是足够小的，但是从推荐实际效果上来讲，序列结果可能是不太好的。

配对法（Pairwise）

配对法（Pairwise）是为了解决单点法无法对序列内商品之间关系建模的问题。其基本思路是对样本进行两两比较，构建偏序商品对，从比较中学习排序。因为对于一个查询关键字来说，最重要的其实不是针对某一个商品的相关性是否估计得准确，而是要能够正确估计一组商品之间的“相对关系”。

在排序模型中，配对法（Pairwise approach）主要学习的是项目之间的相对关系。这种方法的核心思想是将排序问题转化为一系列的配对比较问题，模型通过学习项目对（pair）之间的相对优先级或偏好来进行训练。这与传统的点式（Pointwise）方法不同，后者直接对每个项目进行评分或分类。

在我们开发推荐系统的过程中，一个尚未充分考虑的重要因素是商品之间的相关性。这一点涉及到用户对不同商品的偏好关系。例如，如果一个用户同时浏览了商品A和商品B，我们应该如何判断该用户对哪一件商品的偏好更强？当前的分类系统可能无法精确反映这种偏好差异。因此，我们需要引入配对法来分析和展现商品间的相对关系。这种方法将有助于我们更深入地理解用户的喜好，进而优化推荐效果。

假设有三个商品：A、B和C。完美的排序是“B>C>A”。我们希望通过学习两两关系“B>C”、“B>A”和“C>A”来重构“B>C>A”。但是配对法中的主要问题包括：

1. 完美排序实际上在很多业务场景中是不存在的。
2. 由于推荐序列长度大小不一，导致形成的商品对的数目也不一样，这样会导致模型更加关注长序列商品对模型的影响。

常用算法BPR（贝叶斯个性化推荐）常用于精排模块中（要求商品数要足够少）。

image-20240506165807182

在推荐系统和排序模型的开发中，单点法（Pointwise approach）和配对法（Pairwise approach）分别关注不同的核心要素。单点法主要关注于评分，将推荐问题视作回归或分类问题，直接对每个项目进行评分或分类，适用于需要预测具体评分的场景。而配对法则专注于项目之间的相对关系，通过比较项目对来学习用户的偏好，关注两个项目之间的相对优先级或偏好，更适合于排序和推荐场景，如确定搜索结果的排序或推荐列表中商品的顺序。单点法以其实现的简单性和直接性为优点，但可能无法充分捕捉用户偏好的复杂性；配对法则能够更好地理解用户偏好的细微差别和项目间的相对关系，但计算复杂度较高。

列表法(Listwise)

列表法(Listwise)基本思路是尝试直接优化像 NDCG（Normalized Discounted Cumulative Gain） 这样的指标，从而能够学习到最佳排序结果。但是由于NDCG这类的评估指标实际上是“非连续” 和 “非可微分”，所以直接优化NDCG的这种思路实际上在工业界应用是特别特别少的；常用算法LambdaMART，非必要不建议使用，非要用建议在精排模块中使用(商品要尽可能的少)。

推荐系统本质上是提供一个根据用户偏好排序的商品列表。而进行推荐时，我们不仅仅是分析单个商品的选择概率，还要考虑全局的商品相关性，这就涉及到理解商品列表间的相对关系。理论上，我们完全可以直接基于这个商品列表去构建模型。然而，这种基于列表的模型在实现上会非常复杂，而且在实际应用中可能存在一些限制。因此，尽管这种方法有一定的优势，但我们在这里不再深入讨论。有兴趣的话，大家可以进一步了解并探索这种方法。